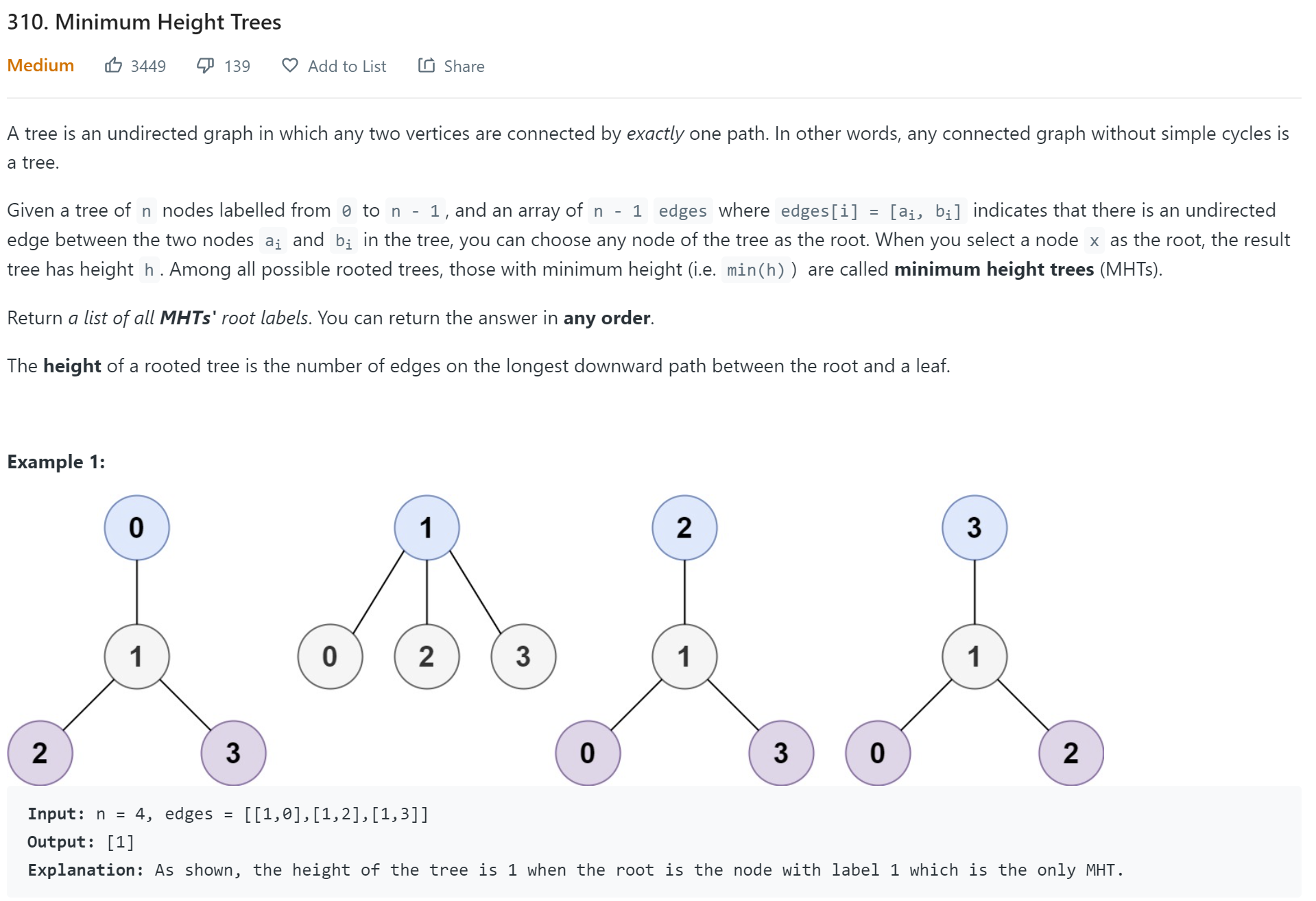
Algorithm & Data Structure - Topological Sort
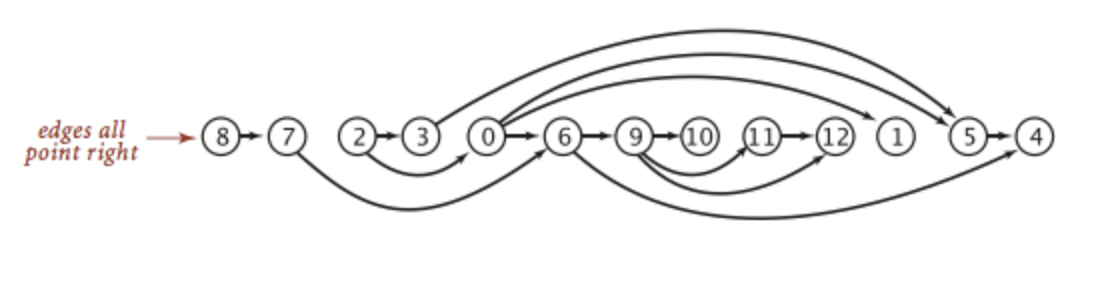
Topological sort is a way to sort a Directed Acyclic Graph (DAG) in the order based on all edge directions. For example, a graph below could be ordered in a way.
A few properties of topological order:
- Only DAG has topological sort, because a cycle is not able decide the sequence of the node;
- Given one DAG, there might be many topological order. Uniqueness of topological order has other restrictions.
- The sort always start from a node with 0 incomming edges.
The main application of topological order is to schedule/arrange tasks and courses, and to find the critical paths.
Uniqueness of topological order
If every consective elements in a topological order is restricted by an edge in the graph, then the topological is unique, i.e., there is no more topological order for this graph.
Number of Topological orders
The number of topological orders for a graph is dependent on the number of subtrees. Assume root node \(r\) has \(n+1\) nodes, then it has \((n+1)!\) to sort all the nodes, however the node orders are restricted by the edges or subtrees. Assume node \(r\) has \(s\) substrees and each subtree has \(k_i\) nodes, each subtree has \(top(i)\) topological sorts. The number of topological sorts of node \(r\) is
\[top(r) = \frac{n!}{k_1!\times k_2! \times ....k_s!} \times \prod_{i=1}^s top(i)\]The basic idea is: there are total \(n+1\) nodes with \((n+1)!\) orders, but the root node is fixed, so now it reduced to total \(n!\) orders, each subtree’s node has \(k_i!\) sorts, but it is replaced by the topological sorts. So divided by \(k_i!\) and multiply by the subtree’s topological sorts.
Algorithms for Topological sort
Kahn’s algorithm
If observe the topological sort carefully, topological sort always starts from root element, i.e., an element without incomming edge/parent/root. This gives the basic idea of Kahn’s algorithm.
- Put all node with 0 incomming edge to a queue/set \(S\);
- For each of the node in \(S\), do:
- Put this node to topological sort set \(T\);
- remove all associated (outgoing) edges of the node;
- remove the edge from the other side of the node;
- if new node with 0 incomming edge is generated, put it into Set \(S\);
- Stop until all node with 0 incomming edge are visited.
- If the graph still has edges, then there is at least one cycle exist;
- Otherwise, output the topological sort.
This algorithm uses BFS to extract the topological sort from the outmost nodes to the innermost nodes. It is like peeling onions.
DFS post order algorithm
Recall post order trasverse is to visit the current node after all its children are visited. This is actually a reverse of topological order. Therefore, it is naturally to use DFS to find topological sort.
for (each node i in graph)
do DFS(i, graph, visited, path)
function DFS(i, graph, visited, path, stack)
if (i is in path) return cycle deteced;
if ( i is visited) return
for ( neighbor of i)
DFS(neighbor, graph, visited, path)
remove i from path
push i to stack
The topological order is the reverse of the stack.
Examples
- Leetcode - 207
This is a straight forward application of topological order algorithm.
public boolean canFinish(int n, int[][] prerequisites) {
List<Integer> [] graph = new List[n];
for (int i = 0; i < n; i++)
graph[i] = new LinkedList<>();
for(int [] req : prerequisites)
graph[req[0]].add(req[1]);
boolean[] visited = new boolean[n];
boolean[] path = new boolean[n];
for (int i = 0; i < n; i++) {
if (!visited[i]) {
if (dfs(i, graph, visited, path)) return false;
}
}
return true;
}
private boolean dfs(int i, List<Integer>[] graph, boolean[] visited, boolean[] path) {
if (i == graph.length) return false;
if (path[i]) return true;
if (visited[i]) return false;
visited[i] = true;
path[i] = true;
for (int nei : graph[i]) {
if (dfs(nei, graph, visited, path)) {
return true;
}
}
path[i] = false;
return false;
}
- Leetcode - 210
Also a straight forward implementation
public int[] findOrder(int n, int[][] prerequisites) {
List<Integer> [] graph = new List[n];
for (int i = 0; i < n; i++)
graph[i] = new LinkedList<>();
for (int [] pre : prerequisites) {
graph[pre[0]].add(pre[1]);
}
boolean[] visited = new boolean[n];
boolean[] path = new boolean[n];
Stack<Integer> courseOrder = new Stack<>();
for (int i = 0; i < n; i++) {
if (!visited[i]) {
if (dfs(i, courseOrder, graph, visited, path)){
return new int[]{};
}
}
}
int[] res = new int[n];
int i = 0;
for (int c : courseOrder) {
res[i++] = c;
}
return res;
}
private boolean dfs(int i, Stack<Integer> courseOrder, List<Integer> [] graph, boolean[] visited, boolean[] path) {
if (i == graph.length) return false;
if (path[i]) return true;
if (visited[i]) return false;
visited[i] = true;
path[i] = true;
for (int nei : graph[i]) {
if(dfs(nei, courseOrder, graph, visited, path))
return true;
}
courseOrder.push(i);
path[i] = false;
return false;
}
- Leetcode - 269
This is also relatively straight forward application of Topological sort. But a few corner cases make this problem difficult to pass all tests:
- Need to check the given word list is actually in order especially when two strings are different lengths with the same prefix.
- If a character has no order information, it could be placed anywhere.
public String alienOrder(String[] words) {
Map<Character, Set<Character>> graph = new HashMap<>();
for (String word : words) {
for (int i = 0; i < word.length(); i++) {
// need to put all character in the map, for corner case 2.
graph.put(word.charAt(i), new HashSet<>());
}
}
for (int i = 0; i < words.length - 1; i++) {
String word1 = words[i];
String word2 = words[i+1];
for (int j = 0; j < word1.length() && j < word2.length(); j++) {
if (word1.charAt(j) != word2.charAt(j)) {
graph.get(word1.charAt(j)).add(word2.charAt(j));
break;
}
}
// corner case 1 above
if (word1.length() > word2.length() && word1.startsWith(word2)) {
return "";
}
}
boolean[] visited = new boolean[26];
boolean[] path = new boolean[26];
Stack<Character> s = new Stack<>();
for (char c : graph.keySet()) {
if (!visited[c-'a']) {
if (dfs(c, s, graph, visited, path)) return "";
}
}
StringBuilder sb = new StringBuilder();
while (!s.isEmpty()) {
sb.append(s.pop());
}
return sb.toString();
}
private boolean dfs(char c, Stack<Character> s, Map<Character, Set<Character>> graph, boolean[] visited, boolean[] path) {
if (path[c-'a']) return true;
if (visited[c-'a']) return false;
visited[c-'a'] = true;
path[c-'a'] = true;
for (char nei : graph.get(c)) {
if (dfs(nei, s, graph, visited, path)) return true;
}
path[c-'a'] = false;
s.push(c);
return false;
}
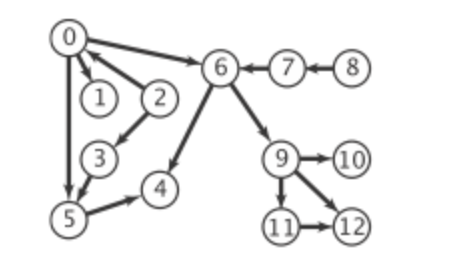
- Leetcode - 310
Direct application of Kahn’s algorithm.
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
// find the degree of all nodes;
// remove all one degree nodes and edge
// until all nodes has only one or 0 degree.
List<Integer> [] graph = new List[n];
for (int i = 0; i < n; i++)
graph[i] = new LinkedList<>();
for (int[] edge : edges){
graph[edge[0]].add(edge[1]);
graph[edge[1]].add(edge[0]);
}
Queue<Integer> q = new LinkedList<>();
List<Integer> res = new LinkedList<>();
for (int i = 0; i < n; i++){
if (graph[i].size() == 1 || graph[i].size() == 0){
q.offer(i);
}
}
while (!q.isEmpty()) {
int size = q.size();
res.clear();
for (int i = 0; i < size; i++) {
int cur = q.poll();
res.add(cur);
if (graph[cur].size() == 0) continue;
int nei = graph[cur].remove(0);
graph[nei].remove(Integer.valueOf(cur));
if (graph[nei].size() == 1) {
q.offer(nei);
}
}
}
return res;
}
Examples - Advanced
In some applications, topological sort need to be combined with dynamical probramming to solve problems. The basic idea is still post order transerve, but need to record and update some state for each node visited.
- Leetcode - 329
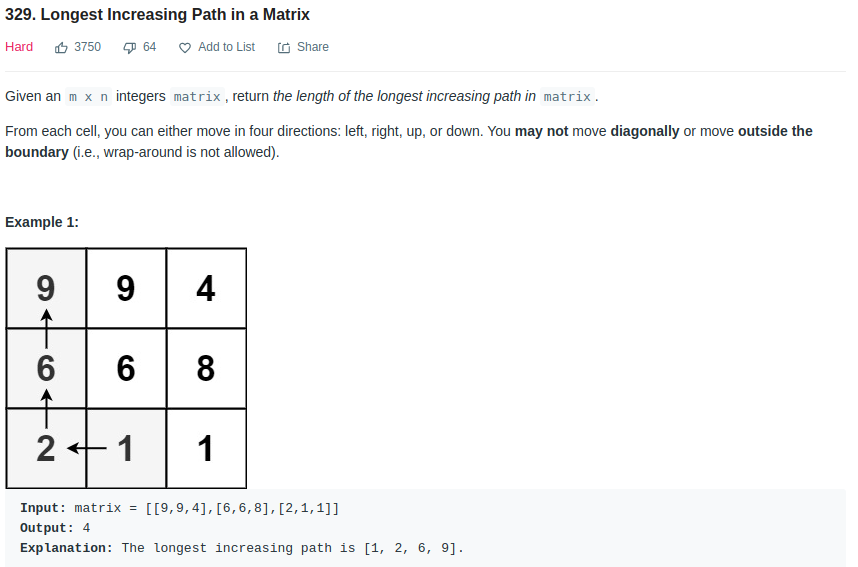
This is basically a graph with one to four neighbors. At any node, its longest increasing path (LIP) is related to its neighbors, which is \(L_{i,j} = max(L_{i+1, j}, L_{i-1, j}, L_{i, j+1}, L_{i, j-1}) if m_{i, j} > neighbor\)
Obviousely, it could be solved recursively until the minimum node is reached, which should return a length of 1. This could also be viewed as a DFS + memory solution.
public int longestIncreasingPath(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
int[][] lsp = new int[m][n];
int maxLSP = 0;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++) {
maxLSP = Math.max(maxLSP, dfs(i, j, lsp, matrix));
}
return maxLSP;
}
private int dfs(int i, int j, int[][] lsp, int [][] matrix) {
if (lsp[i][j] > 0) return lsp[i][j];
int [] dx = new int[]{0, 0, -1, 1};
int [] dy = new int[]{-1, 1, 0, 0};
int curLSP = 1;
for (int k = 0; k < 4; k++) {
int r = i + dx[k];
int c = j + dy[k];
if (r < 0 || c < 0 || r >= matrix.length || c >= matrix[0].length)
continue;
if (matrix[i][j] > matrix[r][c])
curLSP = Math.max(curLSP, dfs(r, c, lsp, matrix)+1);
}
lsp[i][j] = curLSP;
return curLSP;
}
- Leetcode - 851
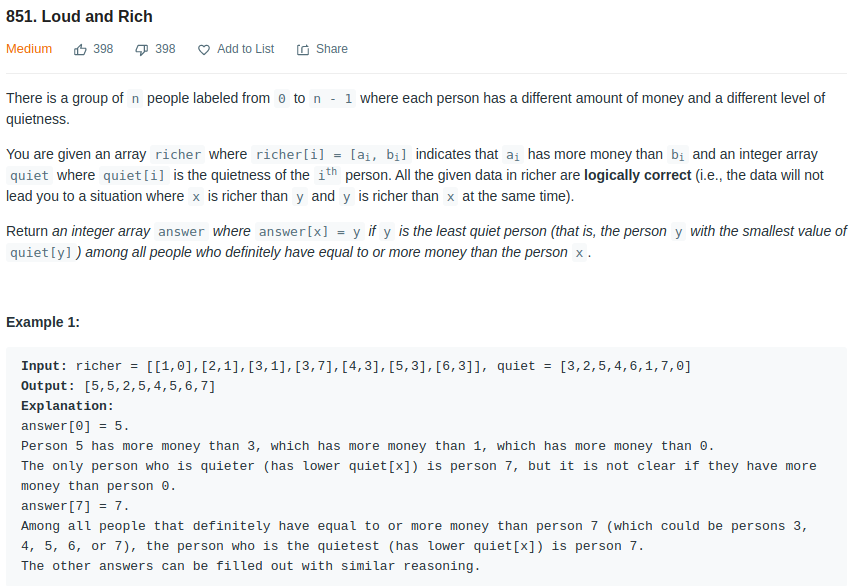
This is similar to the above problem, but the logic is a little bit confusion. The quiteness should be updated from the richest person, because we need to return the quiteness of the person that is richer than current one. So the graph should be build in a way that the richest person is the leave. We also need a map to get the person Id from the quiteness.
public int[] loudAndRich(int[][] richer, int[] quiet) {
//topological sort
int n = quiet.length;
List<Integer> [] graph = new List[n];
for (int i = 0; i < n; i++)
graph[i] = new LinkedList<>();
//graph edge is from richer to poor
for (int[] rich : richer) {
graph[rich[1]].add(rich[0]);
}
int[] ans = new int[n];
Map<Integer, Integer> map = new HashMap<>();
// map from quietness to person Id
for (int i = 0; i < n; i++)
map.put(quiet[i], i);
for (int i = 0; i < n; i++) {
dfs(i, ans, quiet, map, graph);
}
return ans;
}
private int dfs(int i, int[] ans, int[] quiet, Map<Integer, Integer> map, List<Integer> [] graph) {
if (ans[i] > 0) return quiet[ans[i]];
int minQuiet = quiet[i];
ans[i] = i;
for (int rich : graph[i]) {
int rq = dfs(rich, ans, quiet, map, graph);
//select the minimum quietness from person that is richer than current one
if (rq < minQuiet) {
minQuiet = rq;
ans[i] = map.get(minQuiet);
}
}
return minQuiet;
}
- Leetcode - 1857

We need to record maximum color frequency for each path. Naively, we could DFS all path, and record these value. We could improve it by using dynamic programming so that we only need to DFS once. At every node, we record the maximum frequency of all colors of paths that goes from this node. By doing DFS once for the graph, we could find the maximum frequency of colors, we need a 2D array to recorder the colors for all nodes.
public int largestPathValue(String colors, int[][] edges) {
int n = colors.length();
List<Integer> [] graph = new List[n];
for (int i = 0; i < n; i++)
graph[i] = new LinkedList<>();
for (int[] edge : edges) {
graph[edge[0]].add(edge[1]);
}
int[][] colorValue = new int[n][26];
boolean [] visited = new boolean[n];
boolean [] path = new boolean[n];
int maxColorValue = 0;
for (int i = 0; i < n; i++) {
if (!visited[i] && dfs(i, colors, graph, visited, path, colorValue)) return -1;
for (int j = 0; j < 26; j++)
maxColorValue = Math.max(maxColorValue, colorValue[i][j]);
}
return maxColorValue;
}
private boolean dfs(int i, String colors, List<Integer> [] graph, boolean [] visited, boolean[] path, int[][] colorValue) {
if (path[i]) return true;
if (visited[i]) return false;
char c = colors.charAt(i);
visited[i] = true;
path[i] = true;
for (int nei : graph[i]) {
if (dfs(nei, colors, graph, visited, path, colorValue)) return true;
char neiColor = colors.charAt(nei);
//update the color value of current node
for (int j = 0; j < 26; j++) {
colorValue[i][j] = Math.max(colorValue[i][j], colorValue[nei][j]);
}
}
colorValue[i][c-'a']++;
path[i] = false;
return false;
}
- Leetcode - 1916

This is basically to count the number of topological sorts. There are number of smart ways to solve it. A DP with DFS is the way presented here. The big integer is a bit confusion.
private static int mod = 1000000007;
public int waysToBuildRooms(int[] prevRoom) {
int n = prevRoom.length;
List<Integer>[] graph = new List[n];
for (int i = 0; i < n; i++){
graph[i] = new LinkedList<>();
}
for (int i = 1; i < n; i++) {
graph[prevRoom[i]].add(i);
}
long[] factors = new long[n+1];
long[] reverseFactors = new long[n+1];
factors[0] = 1;
for (int i = 1; i <= n; i++){
factors[i] = (factors[i-1]*(long)i)%mod;
reverseFactors[i] = BigInteger.valueOf(factors[i]).modInverse(BigInteger.valueOf(mod)).intValue();
}
boolean[] visited = new boolean[n];
int[][] numWay = new int[n][2];
dfs(0, visited, numWay, graph, factors, reverseFactors);
return numWay[0][0];
}
private int[] dfs(int i, boolean[] visited, int[][] numWay, List<Integer> [] graph, long [] factorial, long[] rFactors) {
if (visited[i]) return numWay[i];
visited[i] = true;
int totalNode = 0;
long numSorts = 1;
long divisor = 1;
for (int subNode : graph[i]) {
int[] subWays = dfs(subNode, visited, numWay, graph, factorial, rFactors);
totalNode += subWays[1];
numSorts = (numSorts*subWays[0])%mod;
divisor = (divisor*rFactors[subWays[1]])%mod;
}
numWay[i][0] = (int)((((factorial[totalNode]*divisor)%mod) * numSorts)%mod);
numWay[i][1] = totalNode + 1;
return numWay[i];
}