Algorithm & Data Structure - Minimum Spanning Tree
Minimum Spanning Tree of a graph has the following properties:
- It has V-1 edges, and all Vertices are connected;
- Add One edge could lead to a cycle in the tree;
- The total weight of the MST is less than any other tree of the graph;
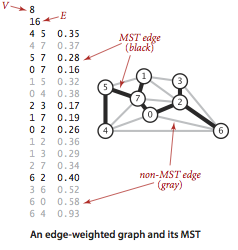
Picture below shows a MST that is from Princeton’s book:
Kruskal’s Algorithm
A natural way to find the MST is using greedy approach that going through all edges from low weight to high, and add the edge if it does not form a cycle in the tree. This is Kruskal’s Algorithm. The problem is how do we detect whether adding a edge forms a cycle. A simple way is to use Union Find: if the vertices of the edges are already connected, then adding it to the tree forms a cycle. Since we need to sort all the edges, the time complexty is \(O(ElogE)\). 1. Sort edges by weight; 2. Select edge from low weight and high weight; 3. If the edge does not form a cycle in the tree, add this edge to the tree; 4. Otherwise, disrecard it.
Prim’s Algorithm
This is similar to dynamic programming approach. Image we have a MST with some vertices and edges, what we could do to grow the tree. If we add an edge and vertex, which edge/vertex should be added to make sure it still be MST? Obviously, we should add the minimum weight edge availabe to the tree, which include all the available edge from the current tree. There are two types implementations that could be used.
Lazy Prim’s Algorithm
- Initialize a Priority Queue, and pick a vertex and add all the edges of the vertex to the queue;
- If the queue is not empty:
- Poll out the minimum edge from the queue;
- If the other vertex of the edge is not visited, add it the tree;
- Add all neighbor edges of the other vertex to the queue. The Priority Queue stores all the edges from the current tree and we always pick the minimum weight edge from it.
This implementation has a time complexity of \(O(ElogE)\)
Eager Prim’s Algorithm
In Lazy implementation, all neighbor edges of a vertex are added to the priority queue which is not actually neccessary. We actually only need to add a edge if the edge weight to the other vertex is less than the existing edge weight to the other vertex from the tree. We could maintain a distTo[] like in Dijkstra algorithm, to record the distance to a vertex from the current MST. If new edge weight (distance) to the vertex is less than old one, then we add it to the priority queue. Note that, here we record the distance from MST to a vertex, not from any source like in Dijkstra algorithm, so we don’t accumlate the weight.
- Initialize a Priority Queue, and distTo[] array;
- Pick a vertex \(i\) and set distTo[i] = 0, and put it to priority queue ordered by distTo;
- If the queue is not empty:
- Poll out the edge with minimum distance from the queue;
- If the other vertex \(j\) of the edge is not visited, add it the tree;
- For all the neighbor edges of the other vertex:
- If the edge weight is less than existing distTo[k], update distTo[k], and put the vertex to the queue. Eager prim’s algorithm reduces the number of edge in the priority queue.
Eager Prim’s algorithm has a time complexity of \(O(ElogV)\).
Application Examples
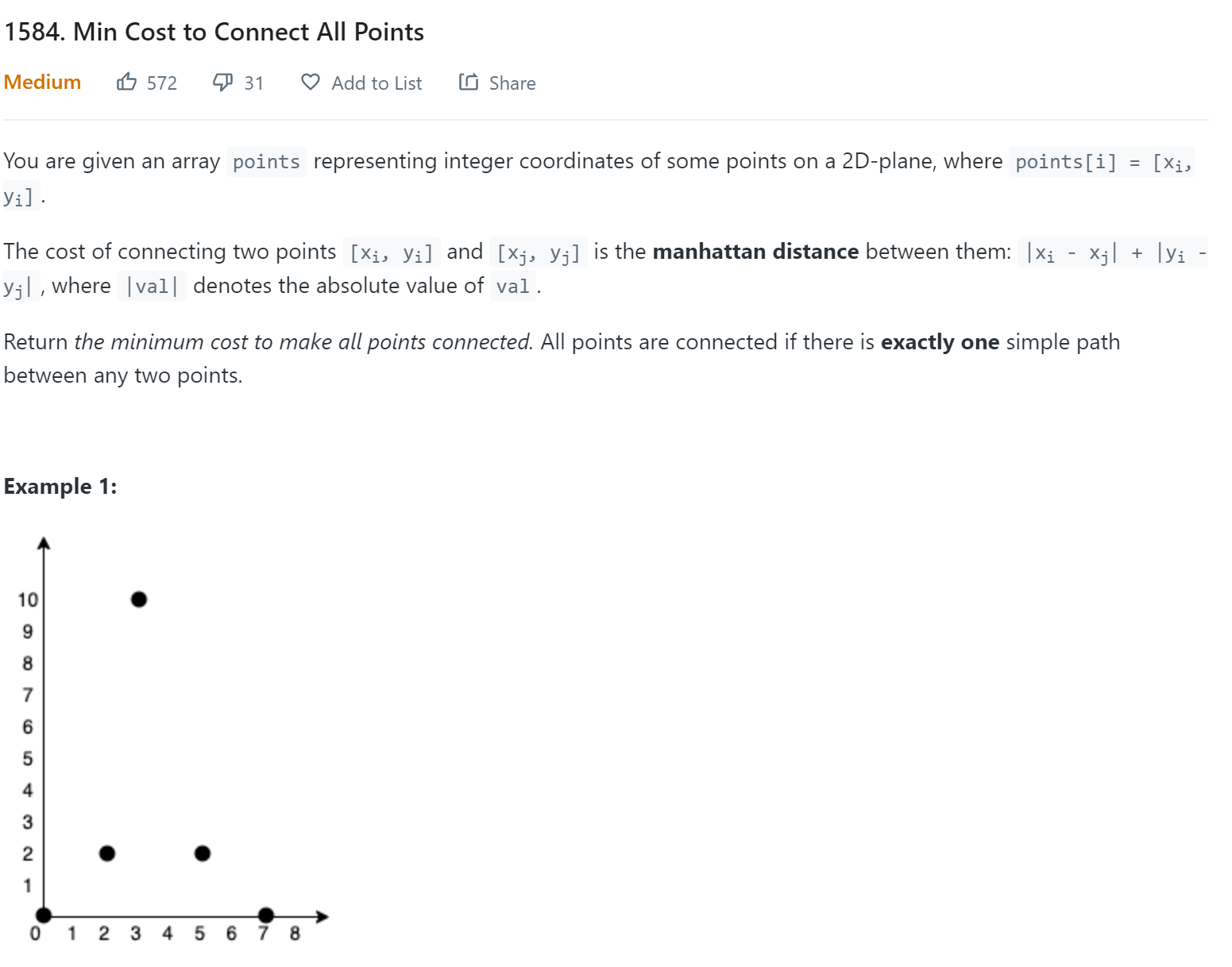
- Leetcode - 1584
The minimum cost is basiclly the weight of the MST. Since every points are connected to other points, this is a dense graph, and Eager’s Prim algorithm gives the best time complexity.
private int eagerPrim(int[][] points) {
//eager prim: only if the distance from the current selected point to the new point has been reduced, add the new distance to the PQ.
int n = points.length;
int[] distTo = new int[n];
Arrays.fill(distTo, Integer.MAX_VALUE);
distTo[0] = 0;
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->x[1]-y[1]);
pq.offer(new int[]{0, 0});
boolean[] visited = new boolean[n];
int cost = 0;
while(!pq.isEmpty()) {
int[] cur = pq.poll();
if (visited[cur[0]]) continue;
visited[cur[0]] = true;
cost += cur[1];
for (int j = 0; j < n; j++) {
int dist = Math.abs(points[cur[0]][0] - points[j][0]) + Math.abs(points[cur[0]][1] - points[j][1]);
if (!visited[j] && distTo[j] > dist) {
distTo[j] = dist;
pq.offer(new int[]{j, distTo[j]});
}
}
}
return cost;
}
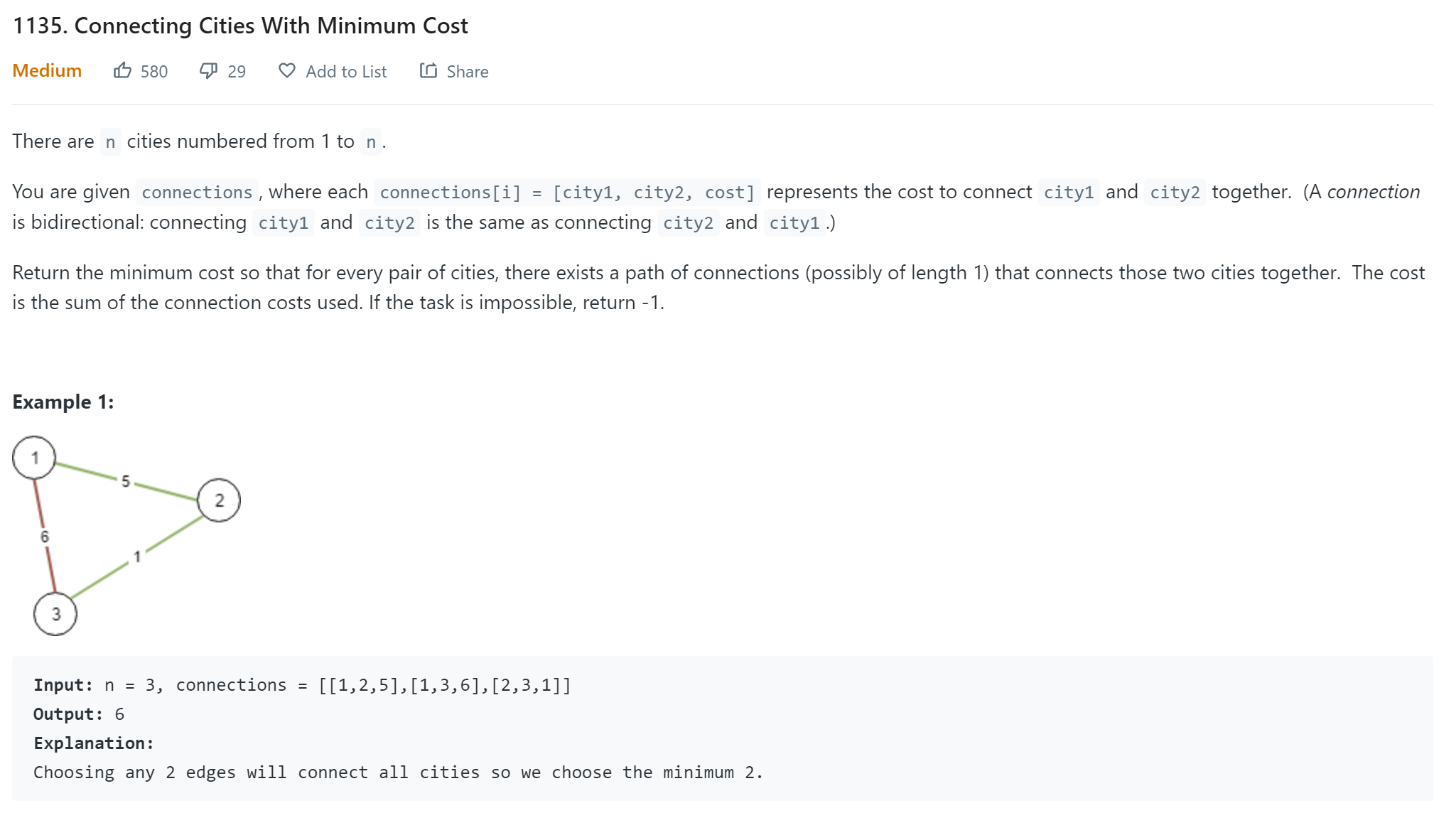
- Leetcode - 1135
Straight MST problem. But note a special case that the city might not be connected. So we need to counts the edges of the MST, if it is not V-1, then return -1. Both Prim and Kruskal could be used.
public int minimumCost(int n, int[][] connections) {
return kruskal(n, connections);
}
private int kruskal(int n, int[][] connections) {
//kruska O(ELogE)
int[] root = new int[n+1];
for (int i = 1; i < n+1; i++)
root[i] = i;
Arrays.sort(connections, (x,y)->x[2]-y[2]);
int cost = 0, edgeCount = 0;
for (int[] conn : connections) {
int u = conn[0];
int v = conn[1];
if (findRoot(root, u) == findRoot(root, v)) continue;
union(root, u, v);
cost += conn[2];
edgeCount++;
}
if (edgeCount == n-1) return cost;
return -1;
}
private int findRoot(int[] root, int u) {
while(root[u] != u) {
root[u] = root[root[u]];
u = root[u];
}
return u;
}
private void union(int[] root, int u, int v) {
int rootu = findRoot(root, u);
int rootv = findRoot(root, v);
root[rootu] = rootv;
}
private int prim(int n, int[][] connections) {
//eager prim O(ELogV)
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->x[1]-y[1]);
int[] distTo = new int[n+1];
Arrays.fill(distTo, Integer.MAX_VALUE);
distTo[1] = 0;
pq.offer(new int[]{1, 0});
List<int[]> [] graph = new List[n+1];
for (int i = 1; i <= n; i++) {
graph[i] = new LinkedList<>();
}
for (int[] conn : connections) {
graph[conn[0]].add(new int[]{conn[1], conn[2]});
graph[conn[1]].add(new int[]{conn[0], conn[2]});
}
int edgeCount = 0;
int cost = 0;
boolean [] visited = new boolean[n+1];
while(!pq.isEmpty()) {
int[] cur = pq.poll();
if(visited[cur[0]]) continue;
visited[cur[0]] = true;
cost += cur[1];
edgeCount++;
for (int[] nei : graph[cur[0]]) {
if (!visited[nei[0]] && distTo[nei[0]] > nei[1]) {
distTo[nei[0]] = nei[1];
pq.offer(new int[]{nei[0], nei[1]});
}
}
}
if (edgeCount == n)
return cost;
return -1;
}
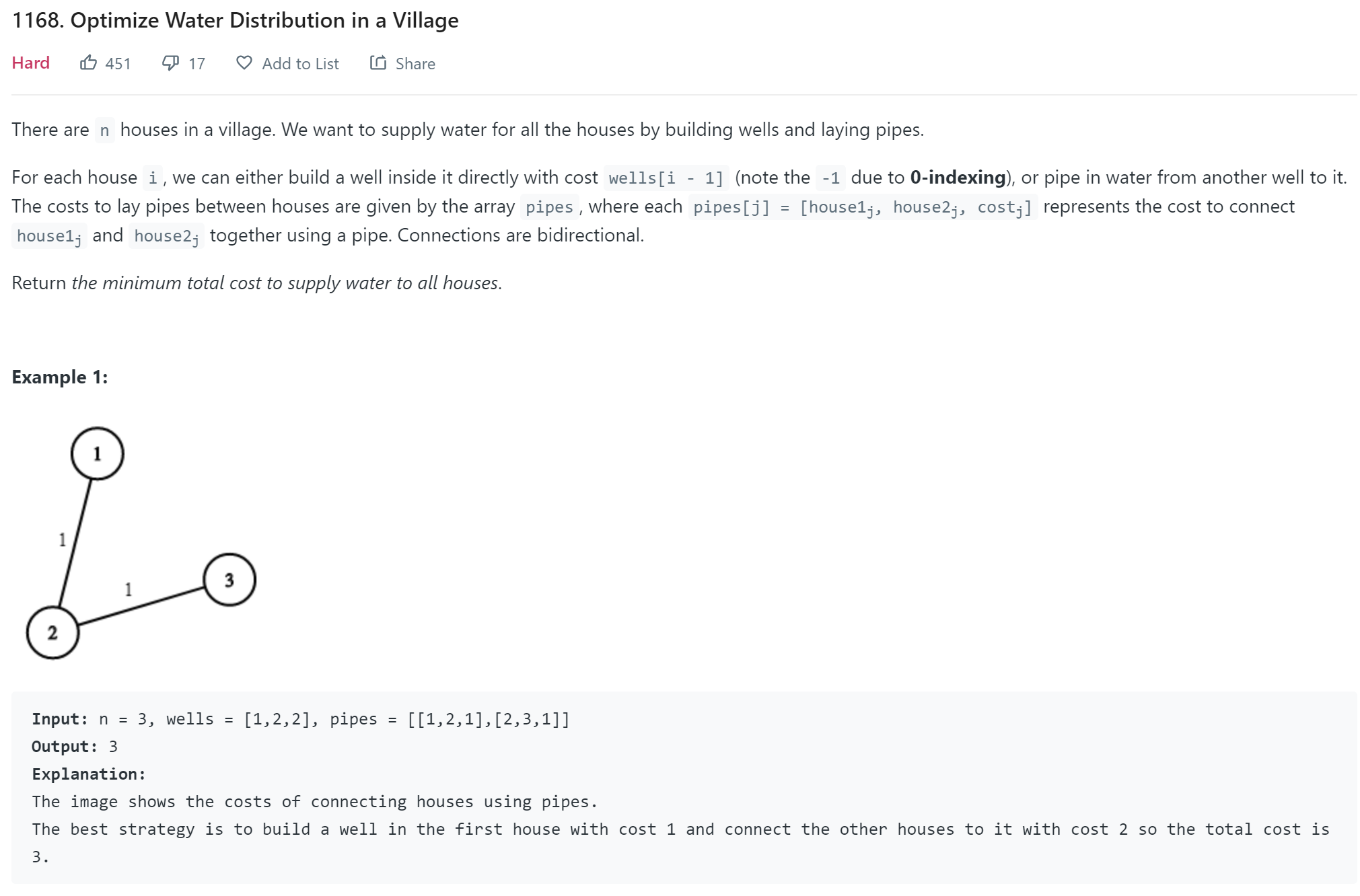
- Leetcode - 1168
Obviously, the pipe network is a MST problem, but how to handle the well cost. At first, I thought the following algorithm:
- Sort the well cost, and pick the minimum to start;
- Extend MST and marked any city connected using Prim algorithm;
- If the next minimum pipe cost is more than any unmarked well cost, then stop and pick the minimum well cost from the unmarked city, start and extend a MST again.
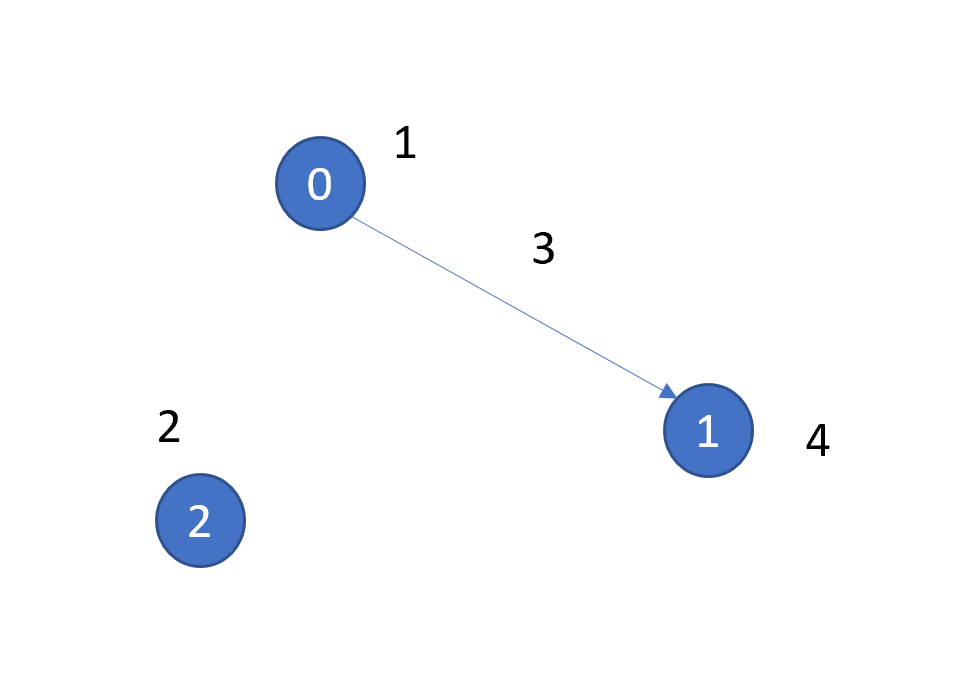
This algorithm works in some cases but not all. Look at the case below, when city 0 is process, the pipe cost from 0 to 1 is more than a city well 2. So the above method stops here and start to expand MST from city 2, and then back to 1 which need to drill a well at city 1. This is not optimal since a pipe from city 0 to city 1 is less than to drill a well at city 1.
Image we only drill one well somewhere, and build pipe to each city with the cost of drilling well to that city. This is the same problem as drill well at a city. We can then build MST based on this new graph.
public int minCostToSupplyWater(int n, int[] wells, int[][] pipes) {
List<int[]> [] graph = new List[n+1];
for (int i = 0; i < n+1; i++)
graph[i] = new LinkedList<>();
for (int [] pipe : pipes) {
graph[pipe[0]].add(new int[]{pipe[1], pipe[2]});
graph[pipe[1]].add(new int[]{pipe[0], pipe[2]});
}
for (int i = 1; i < n+1; i++) {
graph[i].add(new int[]{0, wells[i-1]});
graph[0].add(new int[]{i, wells[i-1]});
}
boolean[] visited = new boolean[n+1];
int[] distTo = new int[n+1];
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->x[1]-y[1]);
int cost = 0;
pq.offer(new int[]{1, 0});
Arrays.fill(distTo, Integer.MAX_VALUE);
distTo[1] = 0;
while(!pq.isEmpty()) {
int[] cur = pq.poll();
if (visited[cur[0]]) continue;
visited[cur[0]] = true;
cost += cur[1];
for (int[] nei : graph[cur[0]]) {
if (distTo[nei[0]] > nei[1]) {
distTo[nei[0]] = nei[1];
pq.offer(new int[]{nei[0], nei[1]});
}
}
}
return cost;
}
- Leetcode - 1489
Simple and straight logic:
- Find MST weight of original graph;
- If remove a edge, we can’t get a MST or MST weight is more than original MST; Then this edge is critical;
- If add a edge to MST wound’t change MST weight, then this edge is pseudo-critical.
Note that when a MST is not exist, that means the weight is Infinity.
public List<List<Integer>> findCriticalAndPseudoCriticalEdges(int n, int[][] edges) {
//Krusal
List<List<Integer>> res = new LinkedList<>();
List<Integer> critical = new LinkedList<>();
List<Integer> pseudoCritical = new LinkedList<>();
Map<int[], Integer> map = new HashMap<>();
for (int i = 0; i < edges.length; i++) {
map.put(edges[i], i);
}
Arrays.sort(edges, (x,y)->x[2]-y[2]);
// MST weight of original graph
int MSTCost = MSTWeight(n, edges, -1, -1);
for (int i = 0; i < edges.length; i++) {
if (MSTWeight(n, edges, i, -1) > MSTCost) {
critical.add(map.get(edges[i]));
} else if (MSTWeight(n, edges, -1, i) == MSTCost) {
pseudoCritical.add(map.get(edges[i]));
}
}
res.add(critical);
res.add(pseudoCritical);
return res;
}
private int MSTWeight(int n, int[][] edges, int skip, int pick) {
int[] root = new int[n];
for (int i = 0; i < n; i++)
root[i] = i;
int countEdge = 0;
int cost = 0;
if (pick != -1) {
cost += edges[pick][2];
countEdge++;
union(root, edges[pick][0], edges[pick][1]);
}
for (int i = 0; i < edges.length; i++ ) {
if (i != skip) {
if (findRoot(root, edges[i][0]) == findRoot(root, edges[i][1])) continue;
countEdge ++;
cost += edges[i][2];
union(root, edges[i][0], edges[i][1]);
}
}
if (countEdge == n-1)
return cost;
return Integer.MAX_VALUE;
}
private int findRoot(int[] root, int u) {
while(root[u] != u) {
root[u] = root[root[u]];
u = root[u];
}
return u;
}
private void union(int[] root, int u, int v) {
int rootu = findRoot(root, u);
int rootv= findRoot(root, v);
root[rootu] = rootv;
}
- Leetcode - 1724
This is similar to shortest path problem but not quite the same. The goal here is to find all the edges that is less than a limit from two vertices, but the path itself doesnot need to be shortest. Therefore, we need to find all the minimum edges from the graphs that not changing the connectivity of the graph itself, which is basically a MST. MST doesn’t change the graph’s connectivity with all edges been minimum possible.
With MST built, we could do BFS or DFS to for each query. There are some better methods, which I will need to explore.
Note that since there is multiple edges in the graph, it is better to handle that by Krustal method, because, Krustal method phases out the larger weight edge naturally.
class DistanceLimitedPathsExist {
private List<int[]>[] graph;
public DistanceLimitedPathsExist(int n, int[][] edgeList) {
graph = new List[n];
for (int i = 0; i < n; i++){
graph[i] = new LinkedList<>();
}
Arrays.sort(edgeList, (x,y)->x[2]-y[2]);
int [] root = new int[n];
for (int i = 0; i < n; i++)
root[i] = i;
for (int[] edge : edgeList) {
if (findRoot(root, edge[0]) == findRoot(root, edge[1])) continue;
union(root, edge[0], edge[1]);
graph[edge[0]].add(new int[]{edge[1], edge[2]});
graph[edge[1]].add(new int[]{edge[0], edge[2]});
}
}
public boolean query(int p, int q, int limit) {
Queue<Integer> queue = new LinkedList<>();
queue.offer(p);
Set<Integer> visited = new HashSet<>();
visited.add(p);
while(!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++){
int cur = queue.poll();
if (cur == q) return true;
for (int[] nei : graph[cur]) {
if (!visited.contains(nei[0]) && nei[1] < limit) {
queue.add(nei[0]);
visited.add(nei[0]);
}
}
}
}
return false;
}
private int findRoot(int[] root, int u) {
while(root[u] != u) {
// root[u] = root[root[u]];
u = root[u];
}
return u;
}
private void union(int[] root, int u, int v) {
int rootu = findRoot(root, u);
int rootv = findRoot(root, v);
root[rootu] = rootv;
}
}