Algorithm & Data Structure - Shortest Path
Shortest Path is a problem that people encounter almost every day. The basic problem statement is: Give a set of vertices and there distance or any measure (a graph), find the shortest path from one source to a target. There might be some variants, for example, to find the minimum cost along a path, but the basic principle and generate approach is the same.
A few properties of the shortest path from the statement above:
- Shortest path doesnot need to cover all vertices;
- There could be multiple shortest pathes;
Brutal Force
The brutal force solution for this problem would be:
- Start from source node s, perform DFS and record all the weight through the path;
- If it reaches to the target node s, comparing it to other paths distance(weight), and select the shortest one. Brutal force could solve the problem, but it takes high time complexibility, about O(V!) where V is the number of vertices.
Bellman-Ford Algorithm
Note that if a graph has only V vertices and E edges, then, the shortest path could be formed by at most V vertices, and V-1 edges, because each vertex could have only one enter and exit edge to form a path. Bellman-Ford algorithm uses this properties of the shortest path.
If we are looking for the shortest path between a pair (u, v) with 0 edge, then obviously, this is INFINITY. With at most 1 edge, then it is the edge weight between u and v if they have edge connected, INFINITY if not. With at most 2 edges, then we can use another vertex in between and comparing to the previous results.

This is dynamic programing approach, built the shortest distance of a pair from 0, and the base case is 0 edge. Following DP approach,
- Initilize a distTo[V][V] matrix, where distTo[i][j] means with at most i edges, the minimum distance from source s to vertex j; Initilize distTo[0][j] = infinity.
- State transition: we already know minimum distance to j with i-1 edges, how to calculate minimum distance to j with i edges ? We only need to add an additional edge, but we don’t know which edge could be added, we try all of them, and test if they could result in less distance to j. for all edges (u, v) if (distTo[i][v] > distTo[i-1][u] + (u,v); update distTo[i][v]; The results is a matrix that gives the minimum distance from source s to all the vertices. We could actually use a one dimension array to record distTo[] and update it every pass.
int[] distTo = new int[V];
Arrays.fill(distTo, Integer.MAX_VALUE);
distTo[s] = 0;
for (int i = 0; i < V-1; i++) {
for (each vertices)
for (Edge edge : graph[v]) {
if (distTo[edge.v] > distTo[edge.u] + edge.w){
distTo[edge.v] = distTo[edge.u] + edge.w;
}
}
}
Time complexity is O(V*E).
Dijkstra algorithm
Dijkstra algorithm uses the fact that if the minimum distance to vertex u is found, then the distance to all its neighbors has high probability to be minimum too. The base case is the distance to source s which is 0, and for every iteration, we get the minimum distance from all non-visited vertices, and update its neighbor. Once a vertex is visited, we don’t need to visit it again. A priority queue could be use to achieve this goal.
int[] distTo = new int[V];
Arrays.fill(distTo, Integer.MAX_VALUE);
distTo[s] = 0;
PQ.add(new int[]{0, 0});
while (!PQ.isEmpty()) {
int[] curVert = PQ.poll();
for (each edge of curVert) {
if (distTo[edge.v] > distTo[edge.u] + edge.w){
distTo[edge.v] = distTo[edge.u] + edge.w;
PQ.add(new int[]{v, distTo[edge.v]});
}
}
}
The best implementation could use index priority queue that is used to change the distance to vertex v in the above code to avoid repeat vertex in the PQ. Java does not provide this option, instead, we could use a Set to record the visited vertex, see below example.
Time complexity: priority queue could have maximum V elements for each edge, so the total complexity is O(ElogV).
Negtive edge and negtive cycle
Dijkstra algorithm does not work for negtive edge and cycle, for negtive edge, it couldn’t find the shortest path. For example like the below graph, at first iteration, the shortest path from A to C is 0, and then C is the next vertex been visited, then B and D. When D is visited, it could update d(B) to -201, but that’s it. It cannot update distance to C, because B has been visited and is not visited again anymore. The actual minimum distance from A to C is -200, but Dijkstra algorithm gives 0.
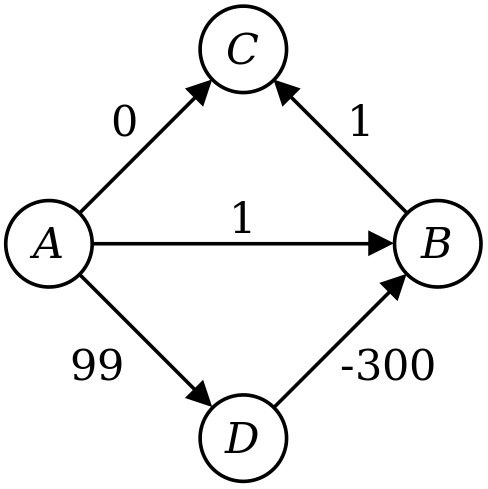
Interestingly, if we remove the restriction of one time for each node, we could get the shortest path using Dijkstra algorithm, but with higher time complexity.
One simple possible solution for negtive edge might be to increase all the edge weights with the absolute of the maximum negtive edge to make all edges positive. But this won’t work, as it changes the weight of all edges, and therefore changes the shortest path too. For example:
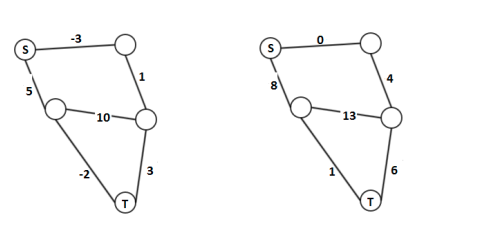
A workable approach is Johnson’s algorithm which alter the reweight the graph using values based on the minimum path solved by Bellman-Ford algorithm. In this way, the relative distance between any two vertices is preserved, and therefore could use to Dijkstra to solve it. This is normally used to solve all pair minimum distance problem, because a single sorce shortest path with negtive weight could be solved by Bellman-Ford algorithm directly.
Bellman-Ford algorithm works for negtive weight but not negtive cycles, because it visit all edges every time. For negtive cycles, both algorithms donot work, since negtive cycle would lead to infinit negtive distance. Bellman-Ford could also be used to detect negtive cycles, after V-1 pass, we could test by doing another pass, and if the any distTo[] could still be reduced, that means there is a negtive cycle in the graph.
Floyd-Warshall algorithm
The above two algorithms find the shortest path between ONE source to all other vertices. If shortest pathes between all pairs of vertices are required, we could loop through all vertices and find the shortest pathes from all vertices to the others. Given the time complexity, and this could give a time complexity of O(VExLogV) for Dijkstra and O(V^2xE) for Bellman-Ford. It might worth a try for sparse graph, but for dense graph, the number of edges \(E=V*(V-1)\), the time complexity would be O(V^3xLogV) for Dijkstra and O(V^4) for Bellman-Ford.
Floyd-Warshall algorithm solves this problem with a guranteed time complexity of O(V^3). The basic thought behind it is similar to Bellman-Ford algorithm. We build the minimum distance from bottom using dynamic progamming approach. Image if we already know the minimum distance between (u, v) that going through vertices (0…i), dist[u][v], what if we add one more vertex to the path i+1, how would it change dist[u][v]? The simple idea is to test whether going through from u to i+1 and to v would reduce previous dist[u][v] that not going through i+1, if yes, then we can update, if not, we keep the old distance. Naturally, with 0 intermidiate vertices, the distance between any two vertices is their edge distance, if no edge connecting them, it is infinity (i.e., with no intermidiate vertex, they cannot reach each other), and this is the base case.
- Initialize a distance matrix between any vertices (i, j), dist[V][V]. Initialize dist[i][j] to edge distance if they are connected directly, otherwise to infinity.
- Loop through 0 to V, and update all pairs of distance, if the current vertices reduces their previous distance.
int[][] dist = new int[V][V]; for (int i = 0; i < V; i++) Arrays.fill(dist[i], Integer.MAX_VALUE); for (int i = 0; i < V; i++) dist[i][i] = 0; for (Edge edge : graph) { dist[edge.u][edge.v] = edge.w; } for (int k = 0; k < V; k++) for (int i = 0; i < V; i++) for (int j = 0; j < V; j++) if (dist[i][j] > dist[i][k] + dist[k][j]) { dist[i][j] = dist[i][k] + dist[k][j]; }Negtive weight and negtive cycle
Floyd-Warshall algorithm is similar as Bellman-Ford algorithm, and it works for negtive edge weight, but not working for negtive cycles. However, it could used to detect negtive cycle. If after all iterations, dist[i][i] < 0, then there is a negtive cycle. The reason is simple, initially, dist[i][i] = 0, if it becomes < 0, then there must be a negtive cycle going through i.
Johnson’s algorithm
As stated above, by adding the absolute of the minimum weight to all the edges would alter the shortest path because the weight is added to every edge. But if we could preserve the relative length of every path and reweight the graph to all positive edge, then we can use Dijkstra’s algorithm to get the shortest path. How could we achieve this? First, we need to obtain the shortest path of each pair of vertices.
- Add a new vertex q to the graph with zero distance to every other vertices;
- Using Bellman-Ford algorithm to find the minimum distance from q to all other vertices h(v).
- Reweight all edges by \(w(u,v) = w(u,v)+h(u)-h(v)\).
- Remove q, and perform Dijkstra algorithm to find the shortest path from any sorce to any target.
Time complexity is O(VExLog(V)) for all pairs of vertices. It is worth for sparse graph.
Examples:
- Leetcode - 743
- Leetcode - 1514
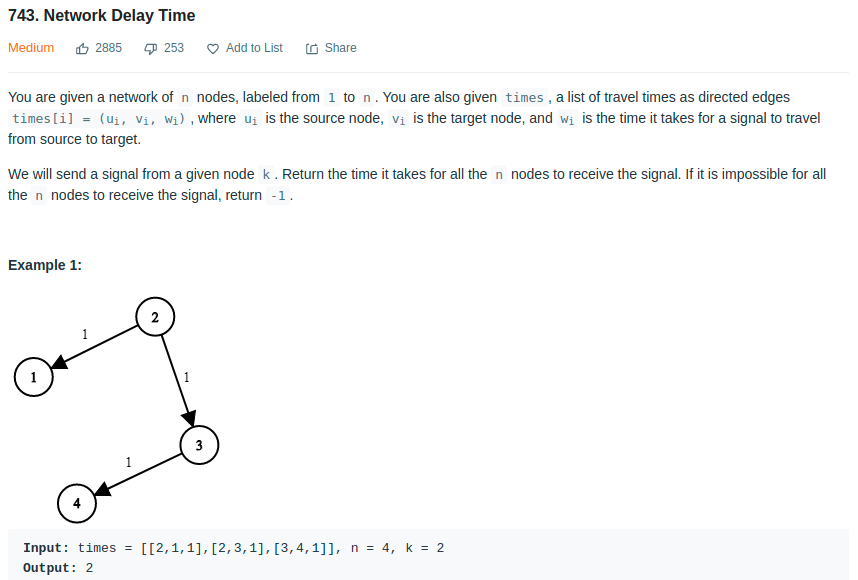
Both problems are typical shortest path examples. Using the first one as an example, the signal passes through the shortest route to all the nodes, and the minimum time for all the nodes to receive the signal is the maximum of all the shortest path. Both Bellman-Ford and Dijkstra algorithms could be used.
//Bellman-Ford Algorithm
public int networkDelayTime(int[][] times, int n, int k) {
int[] timeTo = new int[n];
Arrays.fill(timeTo, Integer.MAX_VALUE);
timeTo[k] = 0;
for (int i = 0; i < n-1; i++) {
for (int [] time : times) {
int u = time[0], v = time[1], w = time[2];
if (timeTo[v] != Integer.MAX_VALUE && timeTo[v] > timeTo[u] + w){
timeTo[v] = timeTo[u] + w;
}
}
}
int maxTime = 0;
for (int i = 1; i <= n; i++) {
maxTime = Math.max(timeTo[i], maxTime);
}
if (maxTime == Integer.MAX_VALUE) return -1;
return maxTime;
}
// Dijkstra algorithm
public int networkDelayTime(int[][] times, int n, int k) {
int[] timeTo = new int[n+1];
Arrays.fill(timeTo, Integer.MAX_VALUE);
timeTo[k] = 0;
List<int[]> [] adj = new List[n+1];
for (int i = 1; i <= n; i++)
adj[i] = new LinkedList<>();
for (int[] time : times) {
adj[time[0]].add(new int[]{time[1], time[2]});
}
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->x[1]-y[1]);
pq.offer(new int[]{k, 0});
Set<Integer> visited =new HashSet<>();
while (!pq.isEmpty()) {
int[] cur = pq.poll();
if (visited.contains(cur[0])) continue;
visited.add(cur[0]);
for (int[] next : adj[cur[0]]) {
if (timeTo[next[0]] > timeTo[cur[0]] + next[1]) {
timeTo[next[0]] = timeTo[cur[0]] + next[1];
pq.offer(new int[]{next[0], timeTo[next[0]]});
}
}
}
int maxTime = 0;
for (int i = 1; i <= n; i++) {
maxTime = Math.max(timeTo[i], maxTime);
}
if (maxTime == Integer.MAX_VALUE) return -1;
return maxTime;
}
- Leetcode - 787

With additional restriction, we need to find the cheapest price with maximum k stops. This restriction changes the ordering in the priority queue, because we should pick a price that satisfies the minimum stop condition. The basic logic is that only if the minimum stop condition is met, we could try to relax its price, and we always select the city with minimum stops. We could of course select based on minimum price, but we have to test the condition of stops.
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
List<int[]> [] graphs = new List[n];
for (int i = 0; i < n; i++)
graphs[i] = new LinkedList<>();
for (int[] flight : flights) {
graphs[flight[0]].add(new int[]{flight[1], flight[2]});
}
int[] priceTo = new int[n];
Arrays.fill(priceTo, Integer.MAX_VALUE);
priceTo[src] = 0;
// order by number of stops in order to handle smaller stops first.
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->{
if (x[2] == y[2]) return x[1]-y[1];
return x[2] - y[2];
});
pq.offer(new int[]{src, priceTo[src], 0});
while (!pq.isEmpty()) {
int[] cur = pq.poll();
if (cur[2] > k) break;
for (int[] next : graphs[cur[0]]) {
if (priceTo[next[0]] > next[1] + cur[1]){
priceTo[next[0]] = next[1] + cur[1];
pq.offer(new int[]{next[0], priceTo[next[0]], cur[2] + 1});
}
}
}
return priceTo[dst] == Integer.MAX_VALUE ? -1 : priceTo[dst];
}
Another way is to order minimum price in the priority queue, but the PQ has to store much more element than the first method, because even with higher price but lower stops, we still need to add it to PQ.
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
List<int[]> [] graphs = new List[n];
for (int i = 0; i < n; i++)
graphs[i] = new LinkedList<>();
for (int[] flight : flights) {
graphs[flight[0]].add(new int[]{flight[1], flight[2]});
}
int[] priceTo = new int[n];
Arrays.fill(priceTo, Integer.MAX_VALUE);
priceTo[src] = 0;
// order the queue with minimum price
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->{
if (x[1] == y[1]) return x[2]-y[2];
return x[1] - y[1];
});
pq.offer(new int[]{src, priceTo[src], 0});
while (!pq.isEmpty()) {
int[] cur = pq.poll();
if (cur[2] > k) continue;
for (int[] next : graphs[cur[0]]) {
//if price is less, add it to PQ, and update priceTo
if (priceTo[next[0]] > next[1] + cur[1]){
priceTo[next[0]] = next[1] + cur[1];
pq.offer(new int[]{next[0], priceTo[next[0]], cur[2] + 1});
} else if (cur[2] + 1 <= k) {
pq.offer(new int[]{next[0], next[1] + cur[1], cur[2] + 1});
}
// if stop still satisfy but price is higher, still need to add to PQ.
}
}
return priceTo[dst] == Integer.MAX_VALUE ? -1 : priceTo[dst];
}
- Leetcode - 1334

This is a problem for shortest pathes between all pair of vertices in graph. Loop through all nodes and apply Dijkstra algorithm could solve it but with high time complexity. Another approach is Johnson’s algorithm.
// Dijkstra algorithm
public int findTheCity(int n, int[][] edges, int distanceThreshold) {
// set each city as src and find the minimum distance from the src
// run Dijkstra for each city O(VE*LogV)
List<int[]> [] graph = new List[n];
for (int i = 0; i < n; i++)
graph[i] = new LinkedList<>();
for (int[] edge : edges) {
graph[edge[0]].add(new int[]{edge[1], edge[2]});
graph[edge[1]].add(new int[]{edge[0], edge[2]});
}
int[] distTo = new int[n];
int minCount = Integer.MAX_VALUE, minId = -1;
for (int i = 0; i < n; i++) {
int curReachable = countReachableCities(i, graph, distTo, distanceThreshold);
if (curReachable <= minCount) {
minCount = curReachable;
minId = i;
}
}
return minId;
}
private int countReachableCities(int src, List<int[]> [] graph, int[] distTo, int maxDist) {
Arrays.fill(distTo, Integer.MAX_VALUE);
distTo[src] = 0;
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->Integer.compare(x[1],y[1]));
pq.offer(new int[]{src, 0});
while(!pq.isEmpty()) {
int[] cur = pq.poll();
if (cur[1] >= maxDist) break;
for (int[] next : graph[cur[0]]) {
if (distTo[next[0]] > cur[1] + next[1]){
distTo[next[0]] = cur[1] + next[1];
pq.offer(new int[]{next[0], distTo[next[0]]});
}
}
}
int count = 0;
for (int dist : distTo) {
if (dist <= maxDist) {
count++;
}
}
return count-1;
}
// Johnson's algorithm
public int findTheCity(int n, int[][] edges, int distanceThreshold) {
int[][] dist = new int[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
dist[i][j] = Integer.MAX_VALUE;
}
for (int i = 0; i < n; i++) dist[i][i] = 0;
for (int [] edge : edges) {
dist[edge[0]][edge[1]] = edge[2];
dist[edge[1]][edge[0]] = edge[2];
}
for (int k = 0; k < n; k++)
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (dist[i][k] != Integer.MAX_VALUE && dist[k][j] != Integer.MAX_VALUE && dist[i][j] > dist[i][k] + dist[k][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
int minCount = Integer.MAX_VALUE, minId = -1;
for (int i = 0; i < n; i++) {
int count = 0;
for (int j = 0; j < n; j++) {
if (dist[i][j] <= distanceThreshold) {
count++;
}
}
if (count <= minCount) {
minCount = count;
minId = i;
}
}
return minId;
}
- Leetcode - 882

This is an application of Dijkstra’s algorithm, we still need to find the minimum distance to reach a node, the weight of each edge is the subnodes on the edge. When we reach a node, we have to decide how many subnodes could be reachable from current node. Once the current node’s distance is more than the threshhold, we can terminate the problem. Be careful on the subnodes that could be visited from the current node, we need to take account of the subnodes that have already been visited before.
public int reachableNodes(int[][] edges, int maxMoves, int n) {
int[] distTo = new int[n];
int[][] subNodes = new int[n][n];
Arrays.fill(distTo, Integer.MAX_VALUE);
distTo[0] = 0;
List<int[]> [] graph = new List[n];
for (int i = 0; i < n; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : edges) {
graph[edge[0]].add(new int[]{edge[1], edge[2]});
graph[edge[1]].add(new int[]{edge[0], edge[2]});
// a matrix to record the nonvisited subnodes from i to j
subNodes[edge[0]][edge[1]] = edge[2];
subNodes[edge[1]][edge[0]] = edge[2];
}
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->x[1]-y[1]);
pq.offer(new int[]{0,0});
Set<Integer> visited = new HashSet<>();
int count = 0;
while(!pq.isEmpty()) {
int [] cur = pq.poll();
if (visited.contains(cur[0])) continue;
visited.add(cur[0]);
if (cur[1] > maxMoves) return count;
count += 1;
for (int[] next : graph[cur[0]]) {
int cnt = subNodes[cur[0]][next[0]];
count += Math.min(cnt, maxMoves-cur[1]);
// update the unvisited subnodes for the edge
subNodes[next[0]][cur[0]] -= Math.min(cnt, maxMoves-cur[1]);
if (distTo[next[0]] > cur[1] + next[1]+1) {
distTo[next[0]] = cur[1] + next[1]+1;
if (distTo[next[0]] <= maxMoves)
pq.offer(new int[]{next[0], distTo[next[0]]});
}
}
}
return count;
}
- Leetcode - 1368

A variation of shortest path problem, this time the cost is the weight between the nodes, and the node is defined by two coordinates, and the neighbors of each node are the adjacent edges of the node.
public int minCost(int[][] grid) {
int m = grid.length, n = grid[0].length;
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->x[2]-y[2]);
pq.add(new int[]{0, 0, 0});
int [] dirX = new int[]{0,0,1,-1};
int [] dirY = new int[]{1,-1,0,0};
int[][] costTo = new int[m][n];
for (int i = 0; i < m; i ++)
for (int j = 0; j < n; j++)
costTo[i][j] = Integer.MAX_VALUE;
costTo[0][0] = 0;
while(!pq.isEmpty()) {
int [] cur = pq.poll();
int x = cur[0];
int y = cur[1];
int cost = cur[2];
if (x == m-1 && y == n-1) return cost;
for (int i = 0; i < 4; i++) {
int nx = x + dirX[i];
int ny = y + dirY[i];
if (nx < m && nx >= 0 && ny < n && ny >= 0 ) {
int nextCost = cost;
if (i != grid[x][y]-1)
nextCost += 1;
if (costTo[nx][ny] > nextCost) {
costTo[nx][ny] = nextCost;
pq.add(new int[]{nx,ny,costTo[nx][ny]});
}
}
}
}
return costTo[m-1][n-1];
}
- Leetcode - 1786

This is an interesting problem. Obviousely, the shortest path from node n to all other nodes need to be calculated using Dijkstra algorithm. The interesting part now is how to count the restricted path.
According to the definition of restricted path, the path should be monotonicly increasing from node n. A DFS approach from node 1 to node n could test all the paths, but that takes high time complexity. DFS with memory solves the problem.
public int countRestrictedPaths(int n, int[][] edges) {
List<int[]>[] adj = (List<int[]> [] ) new LinkedList[n+1];
for (int i = 0; i < n+1; i++) {
adj[i] = new LinkedList<int[]>();
}
for (int[] edge : edges) {
adj[edge[0]].add(new int[]{edge[1],edge[2]});
adj[edge[1]].add(new int[]{edge[0],edge[2]});
}
int[] distTo = new int[n+1];
for (int i = 0; i < n+1; i++) {
distTo[i] = Integer.MAX_VALUE;
}
distTo[n] = 0;
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->x[1]-y[1]);
pq.offer(new int[]{n, 0});
Set<Integer> visited = new HashSet<>();
while(!pq.isEmpty()) {
int [] cur = pq.poll();
if (visited.contains(cur[0])) continue;
visited.add(cur[0]);
for (int[] nei : adj[cur[0]]) {
if (distTo[nei[0]] > cur[1] + nei[1]) {
distTo[nei[0]] = cur[1] + nei[1];
pq.offer(new int[]{nei[0], distTo[nei[0]]});
}
}
}
boolean [] visited = new boolean[n+1];
int[] mem = new int[n+1];
for (int i = 0; i < n+1; i++) {
mem[i] = -1;
}
return dfs(1, n, distTo, adj, visited, mem);
}
private int dfs(int i, int n, int[] distTo, List<int[]>[] adj, boolean[] visited, int[] mem) {
if (i == n) {
return 1;
}
if (mem[i] > -1) {
return mem[i];
}
int count = 0;
visited[i] = true;
for (int[] nb : adj[i]) {
if (visited[nb[0]]) continue;
if (distTo[i] > distTo[nb[0]])
count = (count + dfs(nb[0],n,distTo,adj,visited,mem))%1000000007;
}
visited[i] =false;
mem[i] = count;
return count;
}
After some thought, we could use bottom-up approach to count restrict path. At first, I thought a dynamical programming that update paths from node n to node 1 works, but it does not, because when we update the number of paths of node i, we have to make sure all its neighbours are already updated. It is difficult to ensure that.
int [] dp = new int[n+1];
dp[n] = 1;
for (int i = n-1; i > 1; i--) {
for (int[] nei : adj[i]) {
if (distTo[i] > distTo[nei[0]]) {
dp[i] = (dp[i] + dp[nei[0]])%1000000007;
}
}
}
Then I thought to update the neighbours when we see the node:
int [] dp = new int[n+1];
dp[n] = 1;
for (int i = n-1; i > 1; i--) {
for (int[] nei : adj[i]) {
if (distTo[nei[0]] > distTo[i]) {
dp[nei[0]] = (dp[i] + dp[nei[0]])%1000000007;
}
}
}
It turns out, both ways can’t ensure the paths are counted before update its neighbors.
A simple ways to update the paths is inside Dijkstra algorithm. Note that when we process a node in Dijkstra algorithm, this node is the minimum distance node from the source. That means, its neighbor has two case:
- The neighbor has been processed and its minimum distance is less than the current node;
- The neighbor has not been processed.
Case 1 means this neighbor has less distance to source, and Case 2 means this neighbor MUST have larger distance to source. Therefore, for case 2, the neighbor to current node is a restrict path, we could update the count of pathes for that neighbor.
public int countRestrictedPaths(int n, int[][] edges) {
List<int[]>[] adj = (List<int[]> [] ) new LinkedList[n+1];
for (int i = 0; i < n+1; i++) {
adj[i] = new LinkedList<int[]>();
}
for (int[] edge : edges) {
adj[edge[0]].add(new int[]{edge[1],edge[2]});
adj[edge[1]].add(new int[]{edge[0],edge[2]});
}
int[] distTo = new int[n+1];
for (int i = 0; i < n+1; i++) {
distTo[i] = Integer.MAX_VALUE;
}
distTo[n] = 0;
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->x[1]-y[1]);
int [] dp = new int[n+1];
dp[n] = 1;
pq.offer(new int[]{n, 0});
Set<Integer> visited = new HashSet<>();
while(!pq.isEmpty()) {
int [] cur = pq.poll();
if (visited.contains(cur[0])) continue;
visited.add(cur[0]);
for (int[] nei : adj[cur[0]]) {
// if distTo neighbor is more than current one, this neighbor must have higher distance to current node.
// thus update its count of path by taking all from current node.
if (distTo[nei[0]] > distTo[cur[0]])
dp[nei[0]] = (dp[cur[0]] + dp[nei[0]])%1000000007;
if (distTo[nei[0]] > cur[1] + nei[1]) {
distTo[nei[0]] = cur[1] + nei[1];
pq.offer(new int[]{nei[0], distTo[nei[0]]});
}
}
}
return dp[1];
}
