Algorithm & Data Structure - XOR Operation
XOR Properties
XOR is a bitwise operation that has the following properties:
| x | y | x^y |
|---|---|---|
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
From the above it is easy to deduce: \(x \oplus 0 = 0\) \(x \oplus x = 0\) \(x \oplus y = y \oplus x\)
Of them the most important properties is \(x\oplus x = 0\). A lot of applications are from this properties as below:
In-place swaping
(x, y) => (y, x)
x ^= y => x_1 = x_0^y_0
y ^= x => y_1 = y_0^x_1 = y_0^(x_0^y_0) = x_0
x ^= y => x_2 = x_1^y_1 = (x_0^y_0)^x_0 = y_0
Missing number
- Given an array A of n-1 integers ranging from 1 to n, all number appears once except one number, find this number. *
Using the above property, we could solve it in one pass.
1^2^…..^n ^ A[0] ^ A[1]…..^A[n-1].
All numbers appear two times which is canceled out, except the missing number, which is the result.
Find duplicate number
- Given an array A of n+1 integers ranging from 1 to n, all number appears once except one number twice, find this number. *
Using the the same method above, but this time the number appear three times, so still not canceled out.
XOR with Trie
To find the maximum results of XOR, we could compare bit by bit from the most significant bit, and obtain the maximum results
- Leetcode - 421
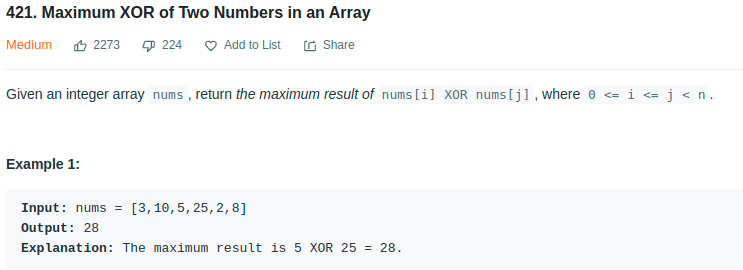
Brutal force takes O(n^2), by using Trie, we could reduce the time complexity to O(n).
- Build Trie for all numbers start from the most significant bit;
- For each of the number in array, find the max XOR by comparing the bit with the bit of trie.
private class TriNode {
TriNode [] children;
TriNode() {
children = new TriNode[2];
}
}
public int findMaximumXOR(int[] nums) {
TriNode root = new TriNode();
//build tri
for (int num : nums) {
insertTri(root, num);
}
int max = 0;
// find maximum xor of each number in the Tri
for (int num : nums) {
max = Math.max(max, maxXor(root, num));
}
return max;
}
private void insertTri(TriNode root, int num) {
TriNode p = root;
for (int i = 31; i >= 0; i--) {
int id = (num>>i)&1;
if (p.children[id] == null) {
p.children[id] = new TriNode();
}
p = p.children[id];
}
}
private int maxXor(TriNode root, int num) {
TriNode p = root;
int max = 0;
for (int i = 31; i >= 0; i--) {
int id = (num >> i) & 1;
//comparing bit
if (p.children[id^1] != null) {
max = max | ( 1 << i);
p = p.children[id^1];
} else {
p = p.children[id];
}
}
return max;
}
- Leetcode - 1938
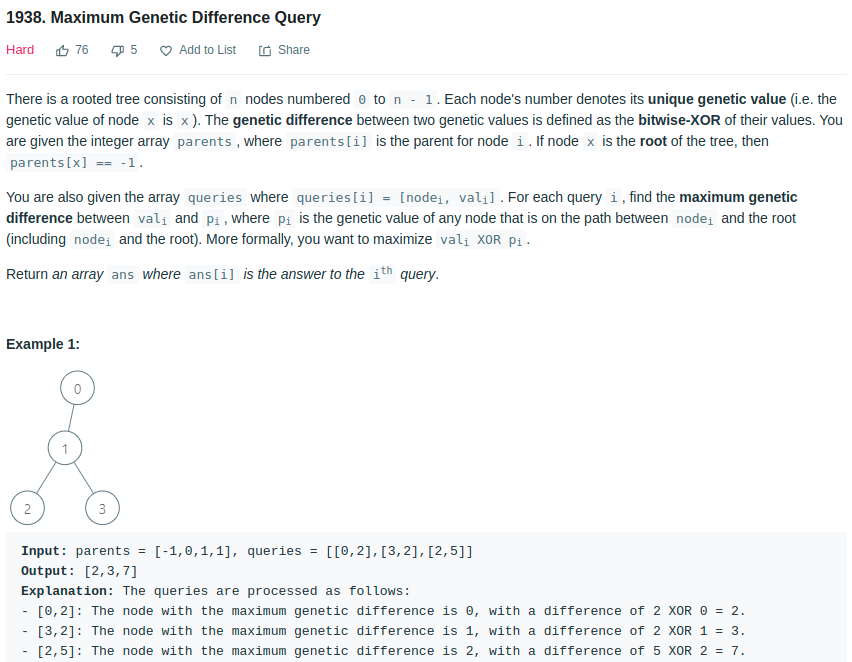
Brutal force takes O(m*n), where m is the tree node, and n is number of queries.
Further thought is to build Tri for all the nodes in the tree, but there is one problem:
- How to compare the query with the path node only;
We could build Tri for each of the path from the queries and the to get the maximum XOR results, but this also cost similar time complexity as brutal force. It seems the path is the key here, and once we get a path, we could get the results for all the queries in the path. We need to keep only one path in the Tri. This is how do we solve it.
- From the tree root, trasverse each path by DFS, and add the current node to the Tri;
- If the current node is a query node, perform find maximum XOR in the Tri;
- Trasverse current nodes’ all children;
- If all children has been visited, remove current node from the Tri.
We need to use a Map to store queries’ node to the query index and value, note that a node could have multiply queries. We also need to store the tree in a way from top root.
private class TriNode {
int count = 0;
TriNode [] children;
TriNode() {
children = new TriNode[2];
}
}
private void insertToTri(TriNode root, int num) {
TriNode p = root;
for (int i = 31; i >= 0; i--) {
int id = (num>>>i) & 1;
if (p.children[id] == null) {
p.children[id] = new TriNode();
}
p = p.children[id];
p.count++;
}
}
private void removeFromTri(TriNode root, int num) {
TriNode p = root;
for (int i = 31; i >= 0; i--) {
int id = (num>>>i) & 1;
p.children[id].count--;
if (p.children[id].count == 0) {
p.children[id] = null;
return;
}
p = p.children[id];
}
}
private int maxXor(TriNode root, int val) {
TriNode p = root;
int max = 0;
for (int i = 31; i >= 0; i--) {
int id = (val>>>i) & 1;
if (p.children[id^1] != null) {
max = max | (1<<i);
p = p.children[id^1];
} else {
p = p.children[id];
}
}
return max;
}
private void dfs(int node, int[] ans, TriNode root, List<Integer> [] adj, Map<Integer, List<int[]>> map) {
insertToTri(root, node);
if (map.containsKey(node)) {
for (int[] query : map.get(node))
ans[query[1]] = maxXor(root, query[0]);
}
for (int next : adj[node]) {
dfs(next, ans, root, adj, map);
}
removeFromTri(root, node);
}
public int[] maxGeneticDifference(int[] parents, int[][] queries) {
//brutal force
List<Integer> [] adj = new List[parents.length];
for (int i = 0; i < parents.length; i++) {
adj[i] = new LinkedList<>();
}
int rootNode = -1;
// build a adjacent matrix
for (int i = 0; i < parents.length; i++) {
if (parents[i] == -1) {
rootNode = i;
} else {
adj[parents[i]].add(i);
}
}
// node map to queries
Map<Integer, List<int[]>> map = new HashMap<>();
for (int i = 0; i < queries.length; i++) {
if (!map.containsKey(queries[i][0]))
map.put(queries[i][0], new LinkedList<>());
map.get(queries[i][0]).add(new int[]{queries[i][1], i});
}
int[] ans = new int[queries.length];
TriNode root = new TriNode();
dfs(rootNode, ans, root, adj, map);
return ans;
}
- Leetcode - 1707

Again, brutal force could take O(m*n), where m is the size of nums, and n is the size of queries.
Using Tri, we could build a number Tri that satisfies the conditions less than m_i. But we need to sort nums and queries first, and build the tri where reach the queries.
public int[] maximizeXor(int[] nums, int[][] queries) {
Map<int[], Integer> map = new HashMap<>();
// put the queries into map before sort them
for (int i = 0; i < queries.length; i++) {
map.put(queries[i], i);
}
//sort nums and queries to build tri on fire
Arrays.sort(nums);
Arrays.sort(queries, (x,y)->Integer.compare(x[1], y[1]));
TriNode root = new TriNode();
int i = 0, j = 0;
int[] ans = new int[queries.length];
while ( j < queries.length) {
//put nums less than m to Tri.
while(i < nums.length && nums[i] <= queries[j][1]) {
insert(root, nums[i]);
i++;
}
if (i == 0) {
ans[map.get(queries[j])] = -1;
} else {
ans[map.get(queries[j])] = maxXor(root, queries[j][0]);
}
j++;
}
return ans;
}
private class TriNode {
TriNode [] children;
TriNode() {
children = new TriNode[2];
}
}
private void insert(TriNode root, int num) {
TriNode p = root;
for (int i = 31; i >= 0; i--) {
int id = (num >>> i) & 1;
if (p.children[id] == null) {
p.children[id] = new TriNode();
}
p = p.children[id];
}
}
private int maxXor(TriNode root, int val) {
int max = 0;
TriNode p = root;
for (int i = 31; i >= 0; i--) {
int id = (val >>> i) & 1;
if (p.children[id^1] != null) {
max = max |(1<<i);
p = p.children[id^1];
} else {
p = p.children[id];
}
}
return max;
}
- Leetcode - 1803
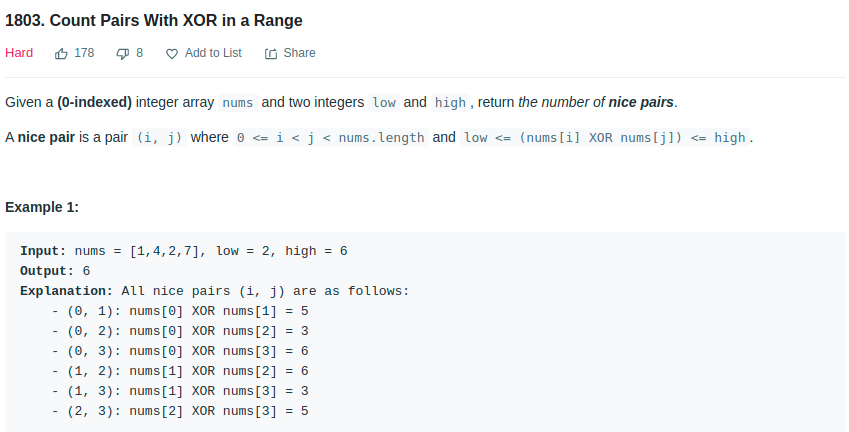
The critical part of this problem is to compare the results of XOR with the low and high values. One thing to note is \(low <= nums[i] XOR nums[j] <= high\) cannot deduce: \(nums[i] ^ low <= nums[j] <= nums[i]^high\)
So we have to compare the XOR result while going through the Tri.
public int countPairs(int[] nums, int low, int high) {
int count = 0;
TriNode root = new TriNode();
//on fly insert nums to the Tri
for (int num : nums) {
int lessHigh = countLess(root, num, high+1);
int lessLow = countLess(root, num, low);
count += lessHigh - lessLow ;
insert(root, num);
}
return count;
}
private class TriNode {
int count = 0;
TriNode [] children;
TriNode() {
children = new TriNode[2];
}
}
private void insert(TriNode root, int num) {
TriNode p = root;
for (int i = 31; i >= 0; i--) {
int id = (num >>> i) & 1;
if (p.children[id] == null)
p.children[id] = new TriNode();
p.children[id].count++;
p = p.children[id];
}
}
private int countLess(TriNode root, int val, int K) {
TriNode p = root;
int count = 0;
for (int i = 31; i >= 0; i--) {
int id = (val >>> i) & 1;
int idK = (K >>> i) & 1;
if (p == null) break;
// comparing bit by bit
if (p.children[0] != null && (id^0) < idK) {
count += p.children[0].count;
} else if (p.children[1] != null && (id^1) < idK) {
count += p.children[1].count;
}
p = p.children[id^idK];
}
return count;
}
