Algorithm & Data Structure - Extreme Value Problem - Type II
This type of problems require to find the maximum/minimum pair from a list or array of values with some conditions. It certainly could be solved by brutal force, but that is not an optimized solution. Swipe from both end of the list or array could help to speed up the process. The basic idea is to reuse the previous information to obtain the current minimum/maximum results. Similar to dynamic programing approach.
- At current location \(i\), previous extreme value upto \(i-1\) is already known;
- By adding \(ith\) element, how to update the extreme value?
Let’s start from a simple example similar to Stock buy sell problem: Find the maximum pair difference from an array.
Brutal force would be simple, two loops give the answer, but it takes O(n^2).
int maxDiff = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
maxDiff = Math.max(nums[i]-nums[j], maxDiff);
}
Look at the inner loop, it starts from 0 for every \(i\). But we already scanned once for all previous elements, can we reuse the previous scan? We can store the minimum value and update it whenever a new element coming. We also need to update the maximum difference.
int maxDiff = 0;
int minNum = nums[0];
for (int i = 1; i < n; i++) {
maxDiff = Math.max(nums[i]-minNum, maxDiff);
minNum = Math.min(minNum, nums[i]);
}
- Leetcode - 1014
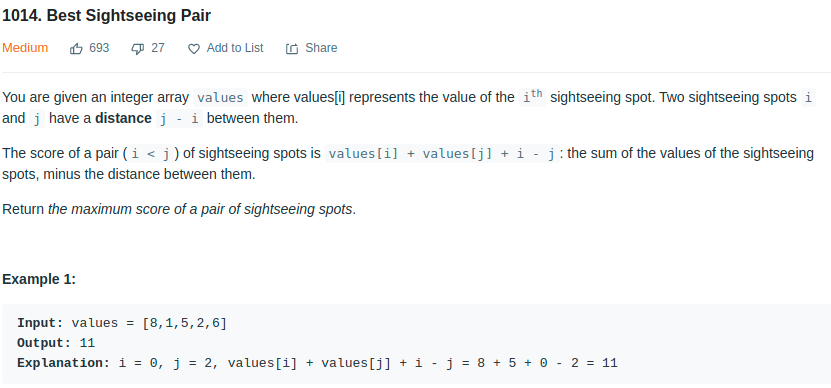
This is similar to find the maximum pair sum with an additional condition. Obviously, two loops solve this problem but with O(n^2). We can use dynamic programming similar above approach to solve it. If we seperate the maximum score into two parts:
\[v_i + v_j + i - j = (v_i + i) + (v_j - j)\]We are looking to maximize these two pars with \(i < j\). So for current \(j\), we only need to use the maximum previous \(v_i+i\) to calculate the current maximum score. This could be done in \(O(1)\) if we keep recording the maximum \(v_i+i\) so far.
public int maxScoreSightseeingPair(int[] values) {
int maxScore = Integer.MIN_VALUE;
int maxNum = values[0];
for (int i = 1; i < values.length; i++) {
maxScore = Math.max(maxScore, values[i]+maxNum-i);
maxNum = Math.max(maxNum, values[i]+i);
}
return maxScore;
}
- Leetcode - 1937
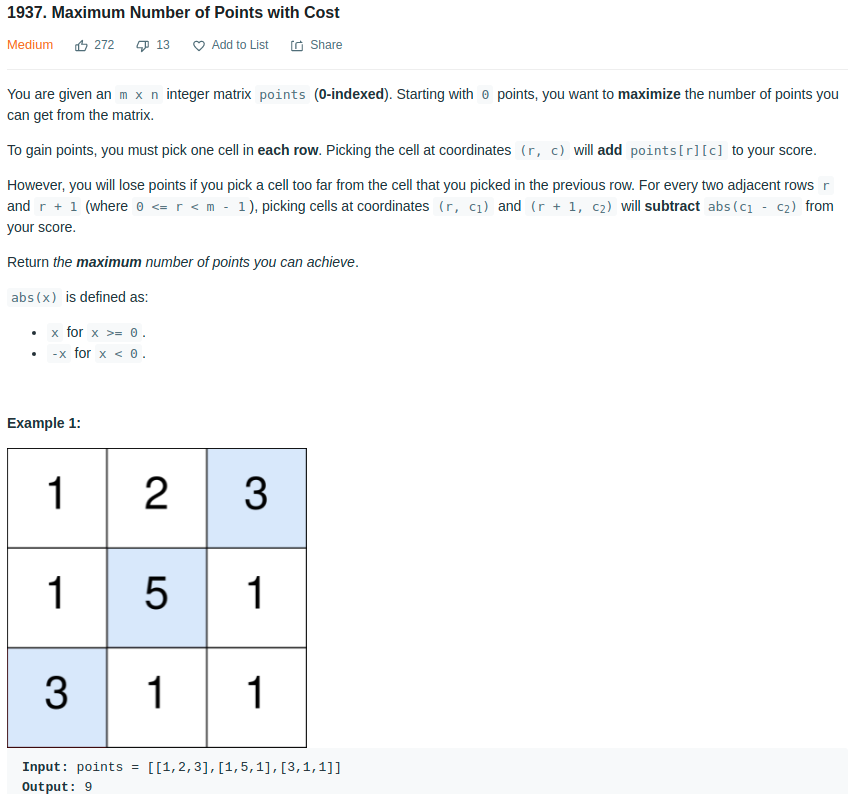
Using dynamic programming, this is relatively easy to get a brutal force solution which takes O(m*n^2). At current point, we calculate the maximum score based on the previous row and current point.
public long maxPoints(int[][] points) {
int m = points.length, n = points[0].length;
long[][] dp = new long[m+1][n];
for (int i = 1; i < m+1; i++) {
for (int j = 0; j < n; j++) {
int curMaxScore = Integer.MIN_VALUE;
for (int k = 0; k < n; k++) {
curMaxScore = Math.max(curMaxScore, dp[i-1][k] + points[i-1][j] - Math.abs(j-k));
}
dp[i][j] = curMaxScore;
}
}
int maxScore = Integer.MIN_VALUE;
for (int j = 0; j < n; j++) {
maxScore = Math.max(dp[m][j], maxScore);
}
return maxScore;
}
The inner third loop is to look for the maximum score for each of the column. If we break the absolute value, we could also seperate the equation into two parts.
\[dp_{i-1, k} + p_{i-1, j} - |j-k| = dp_{i-1, k} + k + p_{i-1, j} - j \quad \textrm{for} \quad j > k \\ dp_{i-1, k} + p_{i-1, j} - |j-k| = dp_{i-1, k} - k + p_{i-1, j} + j \quad \textrm{for} \quad j \leq k\]Now, we only need to update the parts with \(k\) for current \(j\), we could scan from left for \(j>k\) and scan from right for \(j \leq k\), and keep update the maximum score.
public long maxPoints(int[][] points) {
int m = points.length, n = points[0].length;
long[][] dp = new long[m+1][n];
for (int i = 1; i < m+1; i++) {
//scan from left to right
long curMax = dp[i-1][0];
dp[i][0] = dp[i-1][0]+points[i-1][0];
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j] + points[i-1][j];
dp[i][j] = Math.max(dp[i][j], curMax + points[i-1][j]-j);
curMax = Math.max(curMax, dp[i-1][j] + j);
}
//scan from right to left
curMax = dp[i-1][n-1] - (n-1);
for (int j = n-2; j >= 0; j--) {
dp[i][j] = Math.max(dp[i][j], curMax + points[i-1][j]+j);
curMax = Math.max(curMax, dp[i-1][j] - j);
}
}
long maxScore = Integer.MIN_VALUE;
for (int j = 0; j < n; j++) {
maxScore = Math.max(dp[m][j], maxScore);
}
return maxScore;
}
See similar optimization in Stock
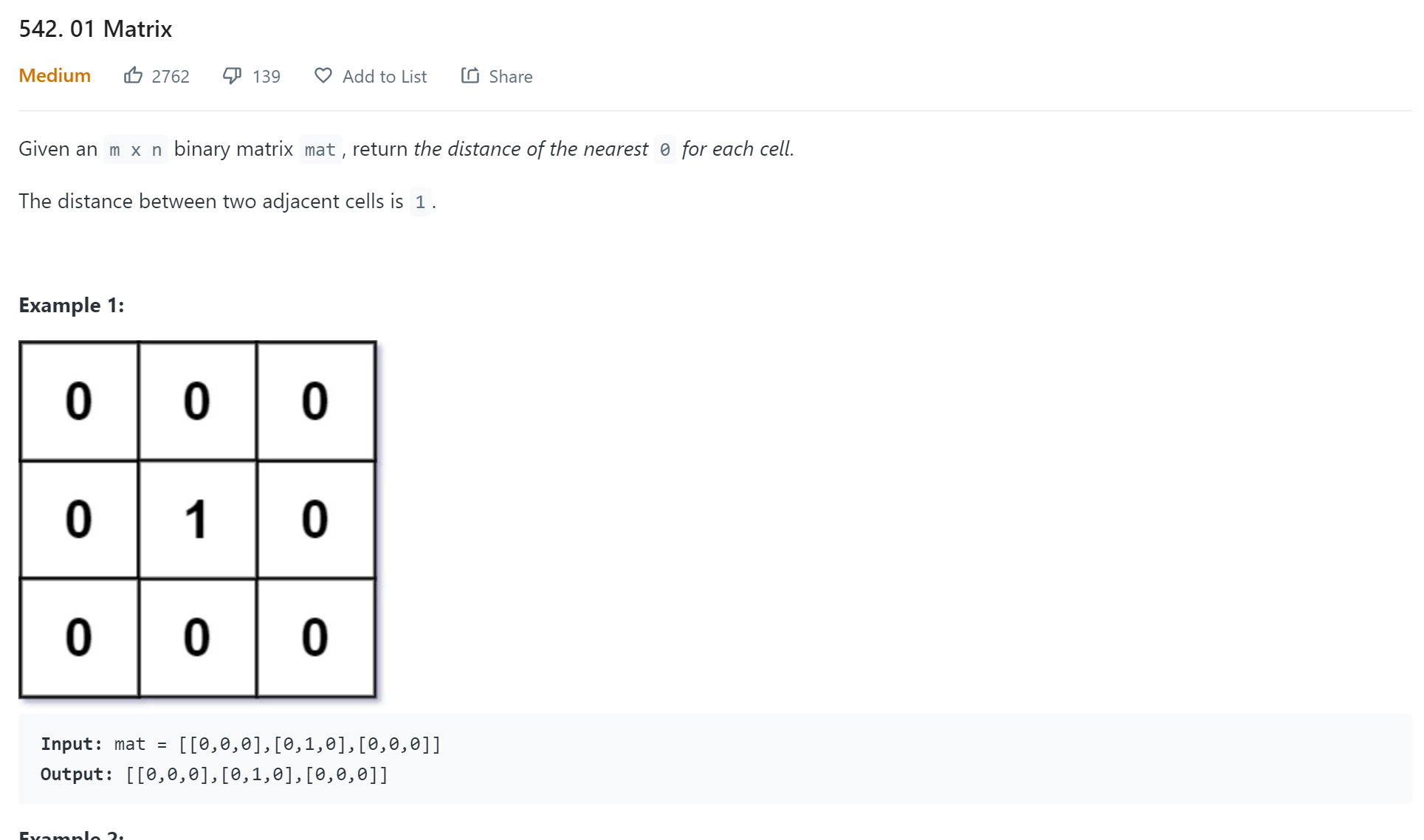
- Leetcode - 542
The first thought is to use DFS, but DFS is not able to get correct value for two consecutive 1s. BFS is able to solve it.
public int[][] updateMatrix(int[][] mat) {
int m = mat.length, n = mat[0].length;
int[][] dist = new int[m][n];
Queue<Integer> q = new LinkedList<>();
Set<Integer> visited = new HashSet<>();
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++){
if (mat[i][j] == 0) {
q.offer(i*n+j);
visited.add(i*n+j);
}
}
int curDist = 0;
while(!q.isEmpty()) {
int size = q.size();
for (int i = 0; i < size; i ++) {
int id = q.poll();
int x = id/n;
int y = id%n;
dist[x][y] = curDist;
int[] dx = new int[]{0, 0, -1, 1};
int[] dy = new int[]{-1, 1, 0, 0};
for (int k = 0; k < 4; k++) {
int r = x + dx[k];
int c = y + dy[k];
if (r >= 0 && r < m && c >= 0 && c < n && !visited.contains(r*n+c)) {
q.offer(r*n+c);
visited.add(r*n+c);
}
}
}
curDist++;
}
return dist;
}
This problem is actually similar to an extreme value problem. It is actually to get the minimum distance to 0 from all its for neighbors. \(d_{i,j} = min(d_{i-1, j}, d_{i, j-1}, d_{i+1, j}, d_{i, j+1})+1 \quad if \quad m_{i,j} = 1\)
Similary, the above equation could be seperated into two part from top left and from right bottom. \(d_{i,j} = min(d_{i-1, j}, d_{i, j-1})+1 \quad if \quad m_{i,j} = 1 \\ d_{i,j} = min(d_{i+1, j}, d_{i, j+1})+1 \quad if \quad m_{i,j} = 1\)
Therefore, we could scan from left top and then from bottom right to get the minimum distance of the current \(i, j\).
public int[][] updateMatrix(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int[][] dist = new int[m][n];
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++) {
if (matrix[i][j] != 0) {
dist[i][j] = Integer.MAX_VALUE-1;
if (i > 0) {
dist[i][j] = Math.min(dist[i][j], dist[i-1][j]+1);
}
if (j > 0) {
dist[i][j] = Math.min(dist[i][j], dist[i][j-1]+1);
}
}
}
for (int i = m - 1; i >=0; i--)
for (int j = n - 1; j >= 0; j--) {
if (matrix[i][j] != 0) {
if (i < m - 1) {
dist[i][j] = Math.min(dp[i][j], ddistp[i+1][j]+1);
}
if (j < n - 1) {
dist[i][j] = Math.min(dp[i][j], dist[i][j+1]+1);
}
}
}
return dist;
}