Algorithm & Data Structure - Sweep Line Algorithm
Sweep line algorithm could be used to solve a number of geometric and interval problem. It normally involves two dimensional sorting. The general idea is to sort one dimension first, and sweep through that dimension to put the other dimension to a binary tree. The basic algorithm is:
- Define Enterning and Leaving event respectively for each of the interval or geometry shape.
- Sort all event by one coordinate (x or y).
- Perform sweep, when an Entering event, put the shape (interval) to a binary tree to sort it.
- When a Leaving event, remove the shape from the binary tree.
The tree could store more than just the dimension data, other required logic could also be performed when entering and leaving the event.
Application
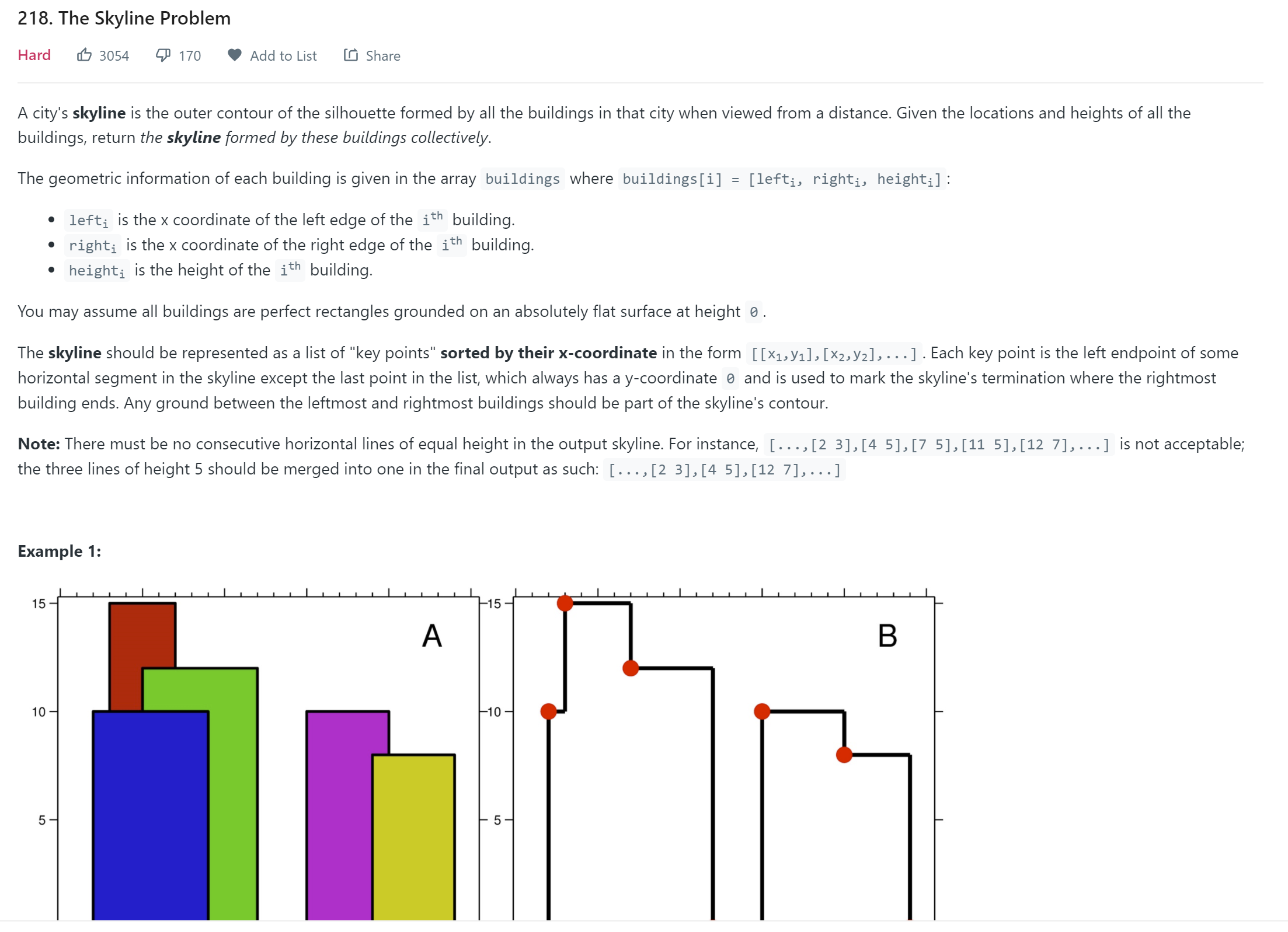
Skyline
- LeetCode - 218
Each rectange has two x value and two y values. We can sort X value first and sweep along X to find Y. Observe the example, we find the skyline needs to mark Y at Entering X if this Y is the strictly maximum, and second largest Y at Leving X if leaving Y is the strictly maximum.
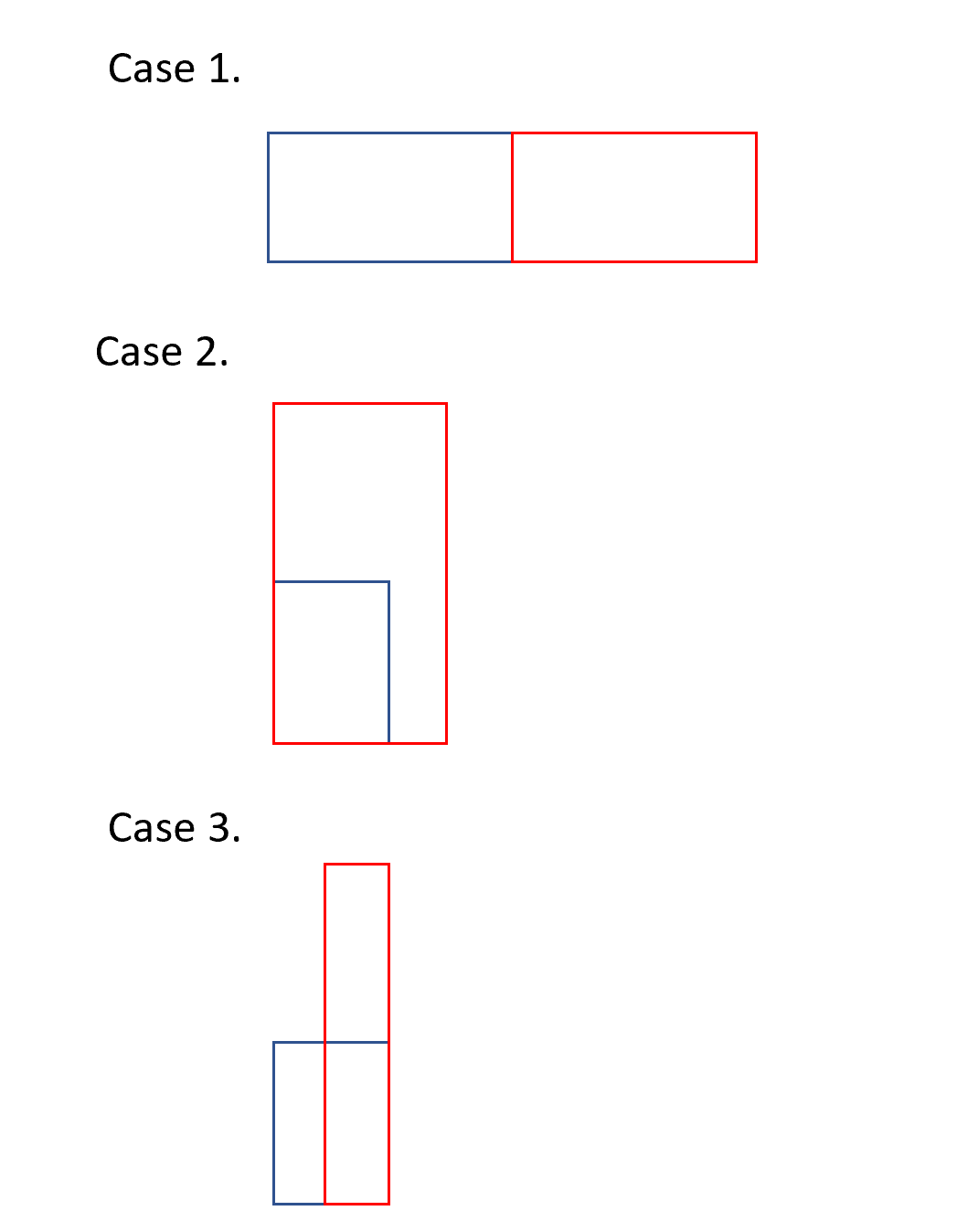
Corner Case 1:
Two rectanges with same Y and consecutive X, i.e., one Leaving (x,y) is the same as the others entering (x,y).
In this case, we shoud not mark this point. We could achieve this by first handle Entering Event, and then Leaving Event. Because when we see Leaving Event, we found the Leaving Y is not strictly maximum.
This corner case also remind that we need to store the times of Y appears.
Corner Case 2:
Two rectanges entering at the same X but different Y. In this case, the smaller Y shound not be marked.
We could achieve this by put the larger Y to the tree first, then the smaller one will not be the maximum when it entering the tree.
Corner Case 3:
Two rectanges leaving at the same X but different Y. Both Y should not be marked. Only the Y next to both leaving Y should be marked.
We could achieve this by leaving the smaller Y first and the larger Y later. In this way, both Y will not be marked.
All these three corner case could be achieve by sort then strategily.
public List<List<Integer>> getSkyline(int[][] buildings) {
//int[]{x, y, event} event 0: entering, event 1: leaving
PriorityQueue<int[]> events = new PriorityQueue<>((x,y)->{
if (x[0]==y[0]) {
if (x[2] == y[2]) {
if (x[2] == 0) return Integer.compare(y[1], x[1]);
if (x[2] == 1) return Integer.compare(x[1], y[1]);
}
return Integer.compare(x[2],y[2]);
}
return Integer.compare(x[0],y[0]);
});
for (int [] building : buildings) {
events.offer(new int[]{building[0], building[2], 0});
events.offer(new int[]{building[1], building[2], 1});
}
// number of heights still in the tree.
TreeMap<Integer, Integer> heights = new TreeMap<>((x,y)->Integer.compare(y,x));
heights.put(0,1);
List<List<Integer>> ans = new LinkedList<>();
while(!events.isEmpty()) {
int[] event = events.poll();
if (event[2] == 0) {
if (event[1] > heights.firstKey()) {
ans.add(new ArrayList<>(Arrays.asList(event[0], event[1])));
}
heights.put(event[1], heights.getOrDefault(event[1],0)+1);
} else {
heights.put(event[1], heights.get(event[1])-1);
if (heights.get(event[1]) == 0) {
heights.remove(event[1]);
}
if (event[1] > heights.firstKey()) {
ans.add(new ArrayList<>(Arrays.asList(event[0], heights.firstKey())));
}
}
}
return ans;
}
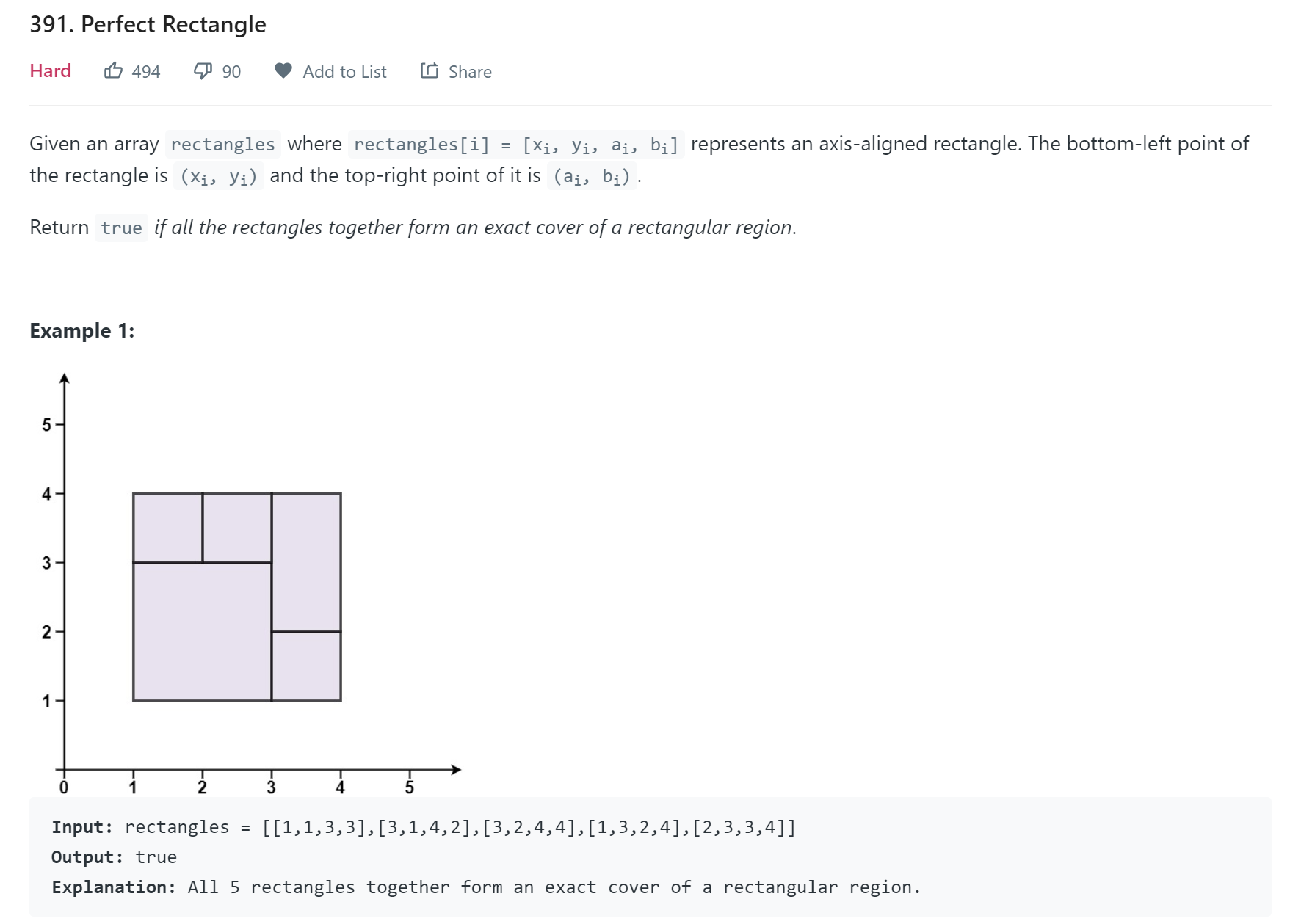
Perfect Rectangle
- LeetCode - 391
A perfect ractangle has no void and no overlap. This implies at every X, the sum of Y should be the same. We could apply the same strategy using sweep line, using Entering and Leaving events. At each X, processing all Entering and Leaving events and calculate the Y range. If it doesnot match the predefined Y range, then return false.
Prefined Y range could be calculated by scaning all rectangles and using the Y_max minus to Y_min.
Corner Case 1
The total sum of range equals predefined Y range, but there is overlap. This could be sovled by store all Y range to a binary tree, and detect overlap in the tree. But this brings a problem that the tree has to remove all Leaving range before it could detect overlap. It could be achieved by sorting the events with leaving events first.
public boolean isRectangleCover(int[][] rectangles) {
//sort events by x, if the same x, leaving event first
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->{
if (x[0] == y[0]) return -1*Integer.compare(x[3],y[3]);
return Integer.compare(x[0],y[0]);
});
int Ymax = 0, Ymin = Integer.MAX_VALUE;
for (int [] rect : rectangles) {
Ymax = Math.max(Ymax, rect[3]);
Ymin = Math.min(Ymin, rect[1]);
pq.offer(new int[]{rect[0], rect[1], rect[3], 0});
pq.offer(new int[]{rect[2], rect[1], rect[3], 1});
}
int Yrange = Ymax - Ymin;
int curYRange = 0;
//Binary tree used to store range and detect overlap range.
// If it is overlaped, return 0 means, elements already in the set.
TreeSet<int[]> range = new TreeSet<>((x,y)->{
if (x[1]<=y[0]) return 1;
if (x[0] >= y[1]) return -1;
return 0;
});
while(!pq.isEmpty()) {
int curX = pq.peek()[0];
while(!pq.isEmpty() && curX == pq.peek()[0]) {
int [] event = pq.poll();
if (event[3] == 0) {
curYRange += event[2] - event[1];
//if an overlap is detected, then return false.
if (!range.add(new int[]{event[1], event[2]})) {
return false;
}
} else {
curYRange -= event[2] - event[1];
range.remove(new int[]{event[1], event[2]});
}
}
if (!pq.isEmpty() && curYRange != Yrange) return false;
}
return true;
}
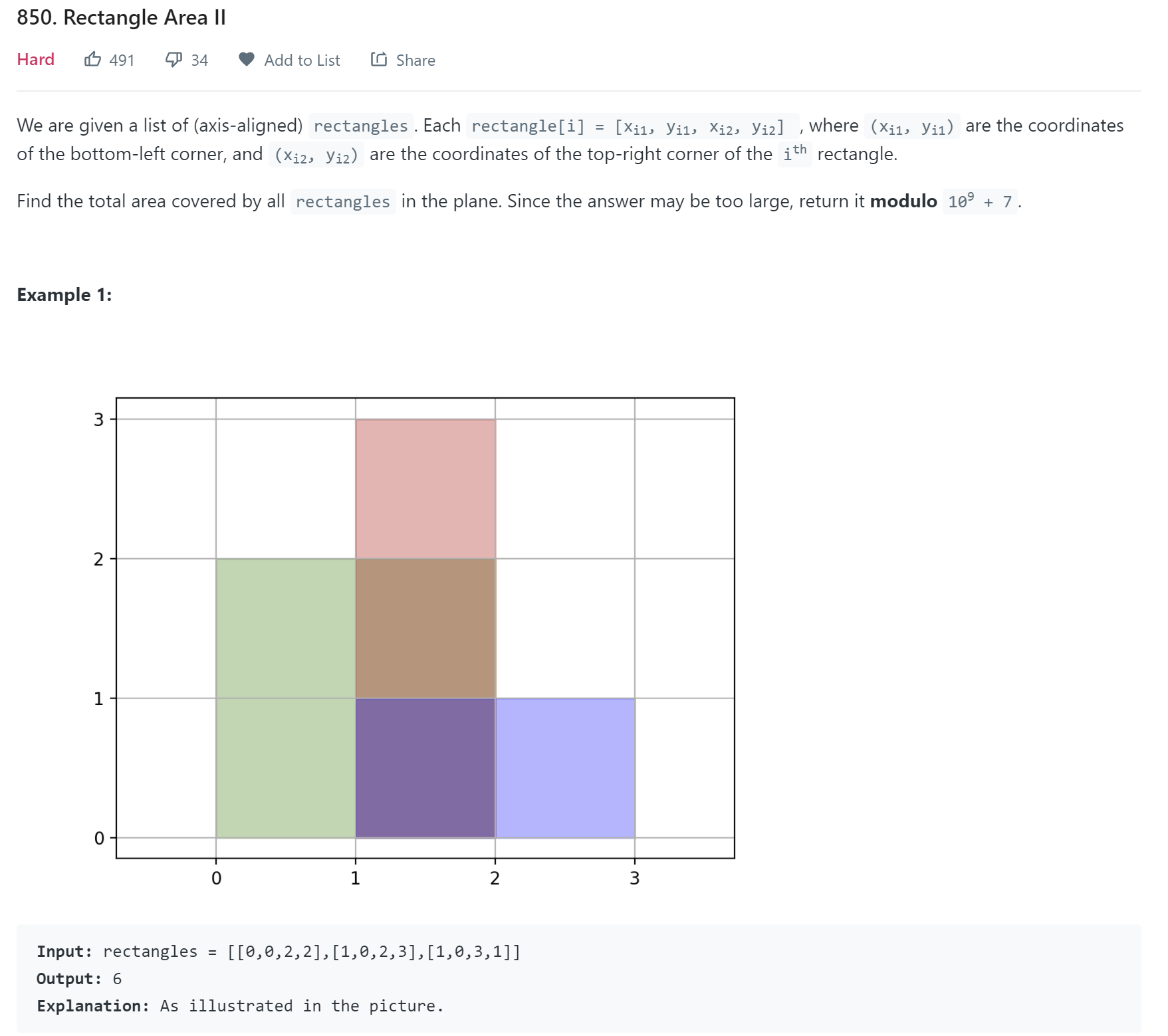
Rectangle Area
- LeetCode - 850
The key is to remove overlap area. We could use sweep line algorithm, whenever we see an event, we calculate the area between previous event and the current event, which is basiclly X coordinate. The area is ( X.cur - X.prev) * Y.range. The question is how to calculate Y range. We could store each of the Y interval in a tree and calculate Y range from the tree.
public int rectangleArea(int[][] rectangles) {
PriorityQueue<int[]> pq = new PriorityQueue<>((x,y)->{
return Integer.compare(x[0],y[0]);
});
for (int [] rect : rectangles) {
pq.add(new int[]{rect[0], rect[1], rect[3], 0});
pq.add(new int[]{rect[2], rect[1], rect[3], 1});
}
TreeMap<int[], Integer> yRangeMap = new TreeMap<>((x,y)->{
if (x[0]==y[0]) return Integer.compare(x[1], y[1]);
return Integer.compare(x[0], y[0]);
});
long area = 0;
long maxYRange = 0;
int prevX = 0;
while (!pq.isEmpty()) {
int curX = pq.peek()[0];
area += (long)(curX - prevX) * maxYRange;
int[] event = pq.poll();
int[] yRange = new int[]{event[1], event[2]};
if (event[3] == 0) {
yRangeMap.put(yRange, yRangeMap.getOrDefault(yRange,0)+1);
} else {
yRangeMap.put(yRange, yRangeMap.get(yRange)-1);
if (yRangeMap.get(yRange)==0)
yRangeMap.remove(yRange);
}
maxYRange = maxYRange(yRangeMap);
prevX = curX;
}
return (int)(area%1000000007);
}
//Calculate Y range from the interval tree
private long maxYRange(TreeMap<int[], Integer> rangeMap) {
long maxRange = 0;
int prev = 0;
for (int[] range : rangeMap.keySet()) {
prev = Math.max(prev, range[0]);
maxRange += Math.max(range[1]-prev,0);
prev = Math.max(prev, range[1]);
}
return maxRange;
}