Algorithm & Data Structure - Word Break
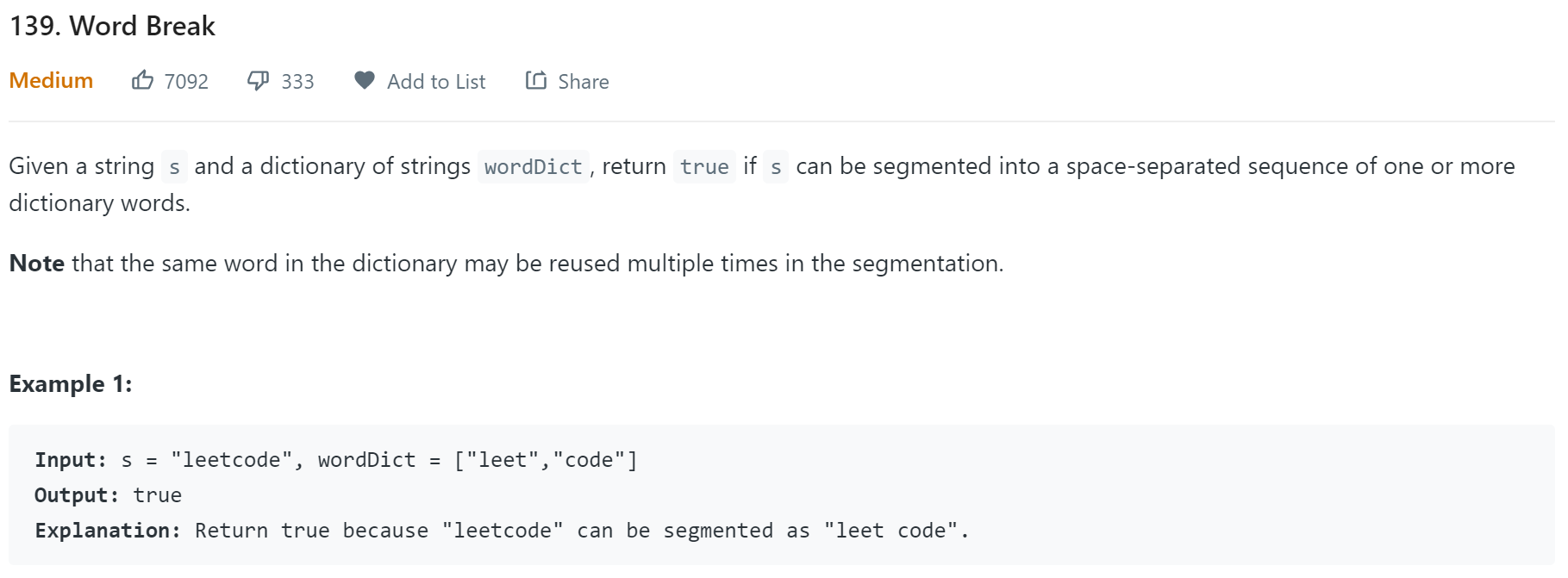
- LeetCode - 139
Brutal Force
Basically, we need to find the points that the string could be broken into words. Brutal force or DFS approach would be to try all substring, time complexity O(n^n), space O(n)
public boolean wordBreak(String s, List<String> wordDict) {
Set<String> set = new HashSet<>();
for (String word : wordDict) {
set.add(word);
}
return dfs(0, s, set);
}
private boolean dfs(int i, String s, Set<String> set) {
if (i == s.length()) return true;
for (int j = i+1; j <= s.length(); j++) {
if (set.contains(s.substring(i, j)) && dfs(j, s, set)) {
return true;
}
}
return false;
}
DFS with Memory
We could add memory to the above solution to save repeated search, this reduces time complexity to O(n^2) with similar space.
public boolean wordBreak(String s, List<String> wordDict) {
Set<String> set = new HashSet<>();
for (String word : wordDict) {
set.add(word);
}
Map<Integer, Boolean> mem = new HashMap<>();
return dfs(0, s, set, mem);
}
private boolean dfs(int i, String s, Set<String> set, Map<Integer, Boolean> mem) {
if (i == s.length()) return true;
if (mem.containsKey(i)) return mem.get(i);
for (int j = i+1; j <= s.length(); j++) {
if (set.contains(s.substring(i, j)) && dfs(j, s, set, mem)) {
mem.put(i, true);
return true;
}
}
mem.put(i, false);
return false;
}
DP method (Bottom up)
Bottom up generally means how could we generate result from previous results. If we already know the answer from \([0...i-1]\), how could we generate result at point \([i]\), i.e., how do we make state transition?
If we know we can form word break from \([0...j]\), then we only need to check if substring \([j+1, i]\) is a word in the dictionary. We could check every \(j\) from \(0\) to \(i-1\). In this way, we checked all possibilities.
public boolean wordBreak(String s, List<String> wordDict) {
HashSet<String> wordSet = new HashSet<>();
for (String str : wordDict) {
wordSet.add(str);
}
boolean [] dp = new boolean[s.length()+1];
dp[0] = true;
for (int i = 1; i < s.length()+1; i++) {
for (int j = 0; j < i; j++) {
if (dp[j] && wordSet.contains(s.substring(j,i))) {
dp[i] = true;
}
}
}
return dp[s.length()];
}
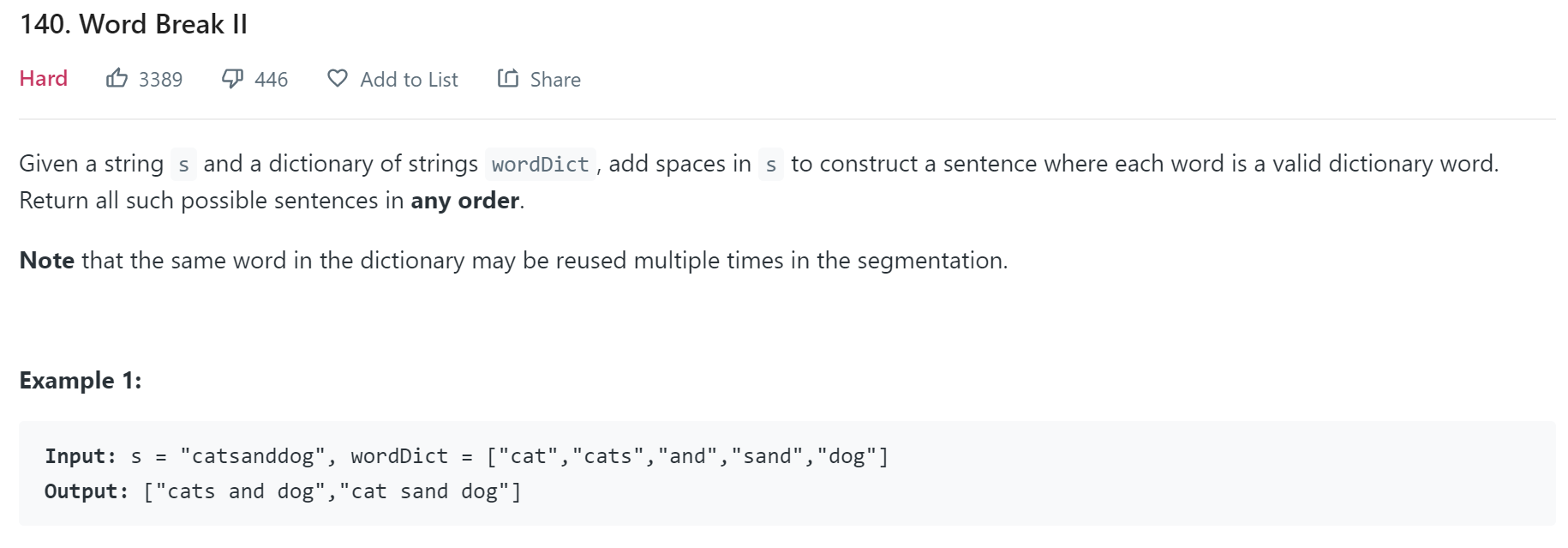
- LeetCode - 140
Since we have to extract all possibility, DFS is a good way to do this job.
public List<String> wordBreak(String s, List<String> wordDict) {
Set<String> wordSet = new HashSet<>();
for (String word : wordDict) {
wordSet.add(word);
}
List<String> res = new LinkedList<>();
dfs(0, s, wordSet, res, new StringBuilder());
return res;
}
private void dfs(int i, String s, Set<String> wordSet, List<String> res, StringBuilder sentence) {
if (i == s.length()) {
res.add(sentence.toString().trim());
return;
}
int curLen = sentence.length();
for (int j = i+1; j <= s.length(); j++) {
if (wordSet.contains(s.substring(i,j))){
sentence.append(s.substring(i,j) + " ");
dfs(j, s, wordSet, res, sentence);
sentence.delete(curLen, sentence.length());
}
}
}
- LeetCode - 472
This is generally a word break question. We need to test whether a word could be broken into other words in the string array. So the problem converts to the first problem above. For each of the word in the array, we could call the method in Leetcode-139 and get an answer.
public List<String> findAllConcatenatedWordsInADict(String[] words) {
List<String> res = new LinkedList<>();
Set<String> wordSet = new HashSet<>();
for (String word : words) {
wordSet.add(word);
}
for (String word : words) {
int n= word.length();
boolean [] dp = new boolean[n+1];
dp[0] = true;
boolean middle = false;
for (int i = 1; i < n+1; i++) {
//note here
for (int j = (i == n ? 1 : 0); j < i; j++) {
if ( dp[j] && wordSet.contains(word.substring(j,i))) {
dp[i] = true;
if (i < n) middle = true;
}
}
}
if (dp[n] && middle) {
res.add(word);
}
}
return res;
}
One corner case need to note is in the inner loop, \(j\) should start from the second letter not the first, because the word itself (without break) is in the set, and if it is start from the first letter, then the word returns true.