Algorithm & Data Structure - Union Find
Union find is a data structure that is like the name defined. Every node in union Find has a root or parent node. It could store the root or father of a node in a array with two operations, union() and find().
- Union: join two nodes together if they are connected;
- Find: find the father or root of a node.
Data Structure
Normally, there is a continous number of nodes \(1 to n\) and it is required to store the connection between these nodes. An array is normally used to store node’s parent or root node. Each node has a parent, and the root’s parent is itself.
Union
Union is to connect two nodes, that means to assign one node to be the other’s parent. In a simplest way, it could be done by one operation O(1). But this will lead the Find operation slow.
Find
Find is to find a node’s root, so that we know whether two nodes are already connected. If they have common root, then ther are connected. Find could take O(n) at worst case if all the nodes are connected, and each of them is unioned in a long chain one by one.
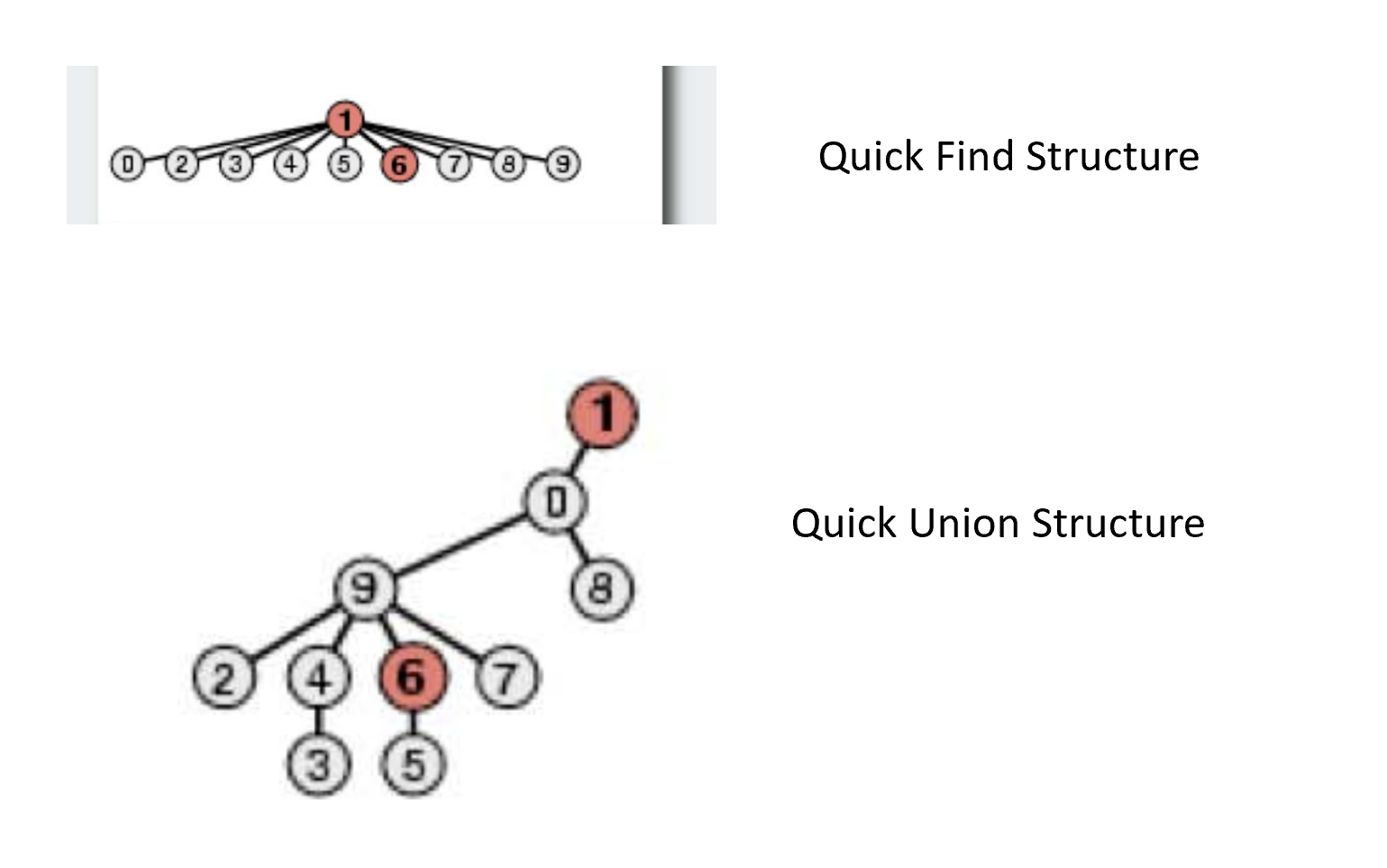
Quick Find
If the data is stored in a way with flat structure, i.e., only two layers exist, one parent and all its nodes are in one flat layer. This makes Find operation very quick O(1) but union operation takes O(n), because we need to update all the son of current node to new parent.
private int find(int[] parent, int u) {
return parent[u];
}
private void union(int[] parent, int u, int v) {
//find parent of u and v
int up = find(parent, u);
int vp = find(parent, v);
// move all the son of vp to under up
for (int i = 0; i < parent.length; i++) {
if (parent[i] == vp) {
parent[i] = up;
}
}
}
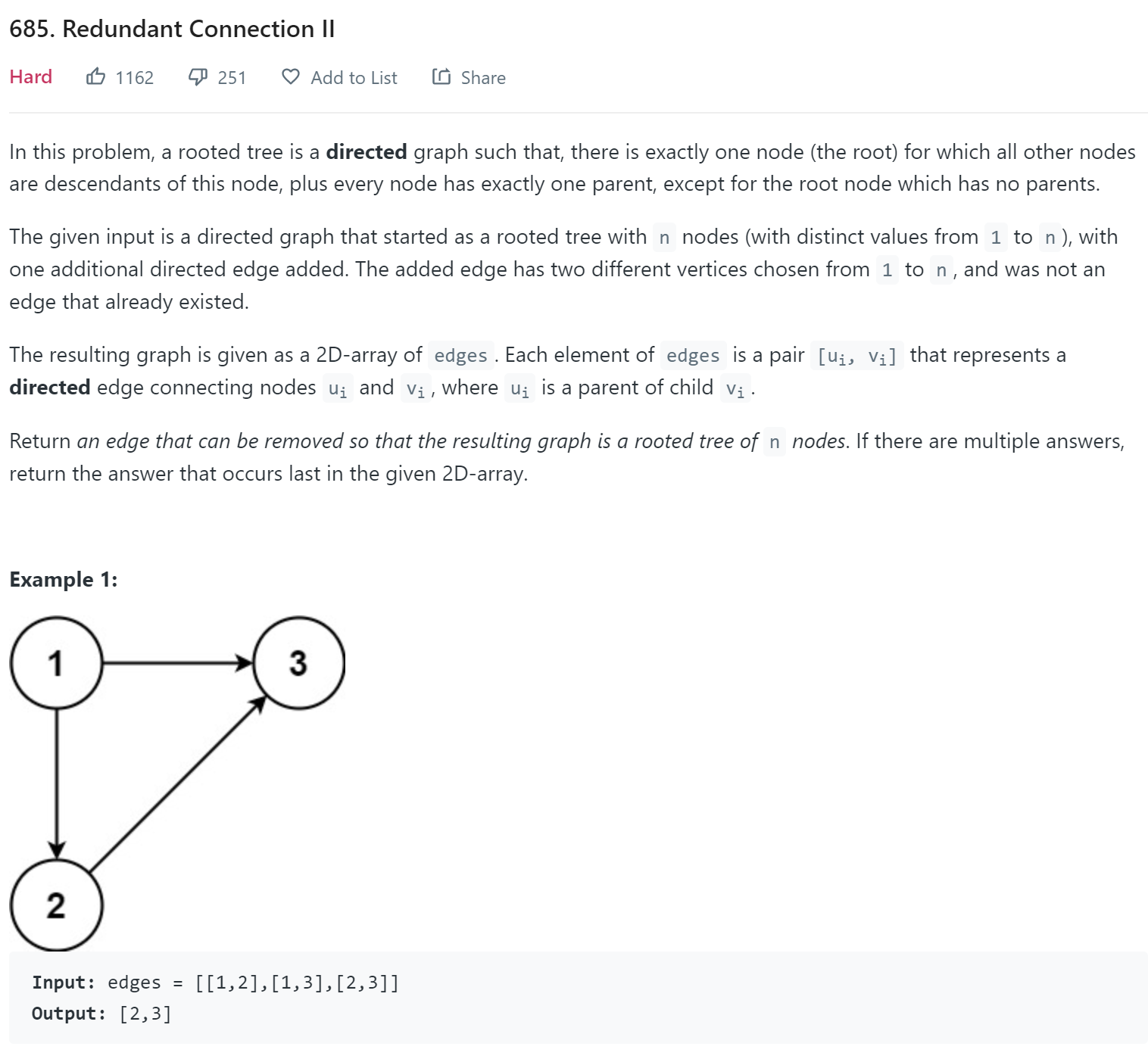
Quick Union
Another way to store the data is to use multiple layers that similar to a tree. If we need to union two subtrees, we could find the root and attach it to another root of node. Both Find and Union operations takes O(h) where h is the height of tree.
private int find(int[] parent, int u) {
while (u != parent[u]) {
u = parent[u];
}
return parent[u];
}
private void union(int[] parent, int u, int v) {
//find parent of u and v
int up = find(parent, u);
int vp = find(parent, v);
parent[up] = vp;
}
Path Compression
Quick Union makes union operation much faster comparing to quick find. But in a worst case, it could take O(n) if all the node is connected to a straight chain. A further optimization is to compress the path from the node to its root. This can be achieved in the Find operation.
private int find(int[] parent, int u) {
while (u != parent[u]) {
// pathe compression
parent[u] = parent[parent[u]];
u = parent[u];
}
return parent[u];
}
private void union(int[] parent, int u, int v) {
//find parent of u and v
int up = find(parent, u);
int vp = find(parent, v);
parent[up] = vp;
}
Application Examples
Redundant Connection
- LeetCode - 684
- LeetCode - 685
This is basically to find the edge that already connected. We have two ways to solve it.
DFS approach
We build the graph as we read edges form input. Before we add the current edge to the graph, we first check whether these two vertices already connected, if it is connected, then this edge could be removed. If not, then we add this edge to the graph. In worst case, it could take O(E(V+E)).
public int[] findRedundantConnection(int[][] edges) {
ArrayList<Integer>[] graph = new ArrayList[edges.length+1];
for (int i = 0; i < edges.length; i++) {
int u = edges[i][0];
int v = edges[i][1];
HashSet<Integer> visited = new HashSet<>();
if (dfs(graph, visited, u, v)) return edges[i];
if (graph[u] == null) graph[u] = new ArrayList<>();
graph[u].add(v);
if (graph[v] == null) graph[v] = new ArrayList<>();
graph[v].add(u);
}
return null;
}
private boolean dfs(ArrayList<Integer> [] graph, HashSet<Integer> visited, int u, int v) {
if (visited.contains(u)) return false;
if (u == v) return true;
if (graph[u] == null || graph[u].size() == 0) return false;
visited.add(u);
boolean connected = false;
for ( int x : graph[u]) {
connected = connected || dfs(graph,visited, x, v);
}
return connected;
}
#### Union Find approach We build union find structure. Wheneven we take a edge from input, we check whether they are already connected by using Find operation. If they are, we find the edge, if not, we union them together. By path compression, it takes O(Elog(V)).
private int[] ufMethod(int[][] edges) {
int[] root = new int[edges.length+1];
for (int i = 0; i < edges.length+1; i++) root[i] = i;
for (int i = 0; i < edges.length; i++) {
int u = edges[i][0];
int v = edges[i][1];
if (find(root,u) == find(root,v)) return edges[i];
union(root,u,v);
}
return null;
}
private void union(int [] root, int u, int v){
int rootU = find(root, u);
int rootV = find(root, v);
if(rootU != rootV) root[rootU] = rootV;
}
private int find(int[] root, int u) {
while(root[u] != u) {
root[u] = root[root[u]];
u = root[u];
}
return u;
}
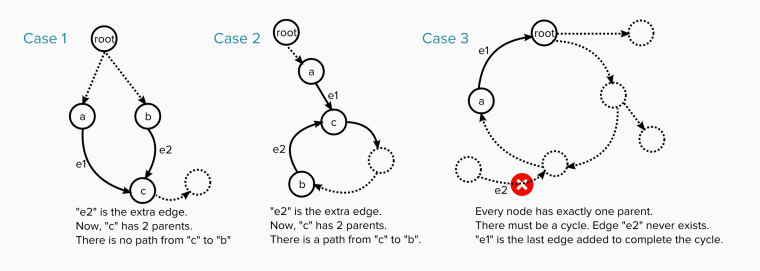
This problem is hard mainly because we have to find out all the corner cases. For undirected tree, we only need to verify if we have cycle in the graph. But in directed tree, three cases might exist that breaks the tree rule:
- One node has two parents (dual parent), break one root rule;
- Directed cycle in graph;
- Both directed cycle and dual parent exist in the graph. Because this problem has only one additional edge exist, Case 3 must be a case that this additional edge forms both directed cycle and dual parent.
Case 1 and 2 are easy to verify seperately. For Case 1, we only need to store each node’s parent, and check if a node has a parent when we see a edge. For Case 2, if we see edge (u, v) we could use DFS or Union Find to verify whether we could reach \(u\) from \(v\).
Case 3 is a little bit triky. If we have a cycle and dual parent two edges, we need to verify which edge is in the cycle, and remove that edge.
That means, if we find a dual parent, we have two potential edges to be removed. If we find a cycle, then another edge could be potentially removed. If we have both dual parent and cycle, we need to verify which dual parent could be removed. A simple approach here is to use only one of the dual parent edge to test whether cycle exists.
DFS approach
public int[] findRedundantDirectedConnection(int[][] edges) {
int n = edges.length;
int[] parent = new int[n + 1];
//edge candidate to be removed
int[] edgeCand1 = null;
int[] edgeCand2 = null;
int[] edgeCand3 = null;
for (int i = 1; i < n + 1; i++) { parent[i] = i; }
List<Integer>[] graph = new LinkedList[n+1];
for (int i = 0; i < edges.length; i++) {
graph[i+1] = new LinkedList<>();
}
for (int i = 0; i < edges.length; i++) {
int u = edges[i][0];
int v = edges[i][1];
// if v already has a parent -- dual parent
// don't put the second edgeCand2 to graph
// use edgeCand1 to test whether cycle exist
if (parent[v] != v) {
edgeCand1 = new int[]{parent[v],v};
edgeCand2 = edges[i];
continue;
}
if (dfs(v, u, graph)) {
// if cycle exist, this edge is a candidate
edgeCand3 = edges[i];
}
graph[u].add(v);
parent[v] = u;
}
// now select a edge to remove
// if no dual parent, then the last edge forming cycle is removed
if (edgeCand1 == null) return edgeCand3;
//if no cycle, then remove the last edge that forms dual parent (note, the graph doesn't include edgeCand2)
if (edgeCand3 == null) return edgeCand2;
//if both dual parent and cycle exist, because the graph includes edgeCand1 in the cycle (edgeCand1 also forms dual parent), remove it.
return edgeCand1;
}
private boolean dfs(int u, int v, List<Integer>[] graph) {
if (u == v) return true;
for (int next : graph[u]) {
if (dfs(next, v, graph)) {
return true;
}
}
return false;
}
Union Find approach
Union Find has similar logic, but save time in verify cycle, which results in time complextity O(ELog(n))
public int[] findRedundantDirectedConnection(int[][] edges) {
int n = edges.length;
int[] parent = new int[n + 1];
int[] root = new int[n+1];
int[] edgeCand1 = null;
int[] edgeCand2 = null;
int[] edgeCand3 = null;
for (int i = 1; i < n + 1; i++) { parent[i] = i; root[i] = i;}
for (int i = 0; i < n; i++) {
int u = edges[i][0];
int v = edges[i][1];
// case 1: dual parent
// case 2: has cycle
// case 3: dual parent and has cycle
// if v already has a parent -- dual parent
// don't put the second edgeCand2 to graph
if (parent[v] != v) {
edgeCand1 = new int[]{parent[v],v};
edgeCand2 = edges[i];
continue;
}
if (root(root, u) == root(root,v)) {
edgeCand3 = edges[i];
}
union(parent, root, u, v);
}
// if no dual parent, then remove edge that forms cycle
if (edgeCand1 == null) return edgeCand3;
if (edgeCand3 == null) return edgeCand2; //if no cycle, then remove the last edge that forms dual parent
return edgeCand1; //if both edgeCand1 and edgeCand3 are not null, then edgeCand1 forms both cycle and dual parent
}
private int root(int[] root, int u) {
while (root[u] != u) {
root[u] = root[root[u]];
u = root[u];
}
return u;
}
private void union(int[] parent, int[] root, int u, int v) {
parent[v] = u;
root[v] = u;
}