There are a series of interesting subsequence related problems that shares some common approach to solve them. This is a summary of them and shall be updated continuously.

Arithmetic slice

Problem Statement

Brutal force

It is intuitive to get a brutal force solution using backtracking method: Generate all subsequence and check if the subsequence is arithmetic or not. This will take O(2^n).

Dynamic programming

A further thinking in this problem is: we are looking for the same difference for all elements. So we can store the difference between any two elements, and find the number of same difference that we can get. We can use a HashMap to recorder the number of the same differences.

When we move to element \(i\), we take the difference between \(i\) to all precede element \(j\) (because we are looking subsequence), and go back to HashMap to see how many same difference we have at element \(j\). If we get \(k\) from element \(j\), then element \(i\) could be combined to form \(k\) subsequence with same difference. Then we update the number of same difference to the current element \(i\). Because, we need to check all the precede elements, we will need to a HashMap at every node. For example:

2 4 6 8 10

For element \(4\), we don’t have any difference generated before. For element \(6\), at previoud element \(4\), we generate a new difference \(2\), and we already have a different \(2\) till element \(4\), so element \(6\) could form subsequence with element \(4\) and previous elements.

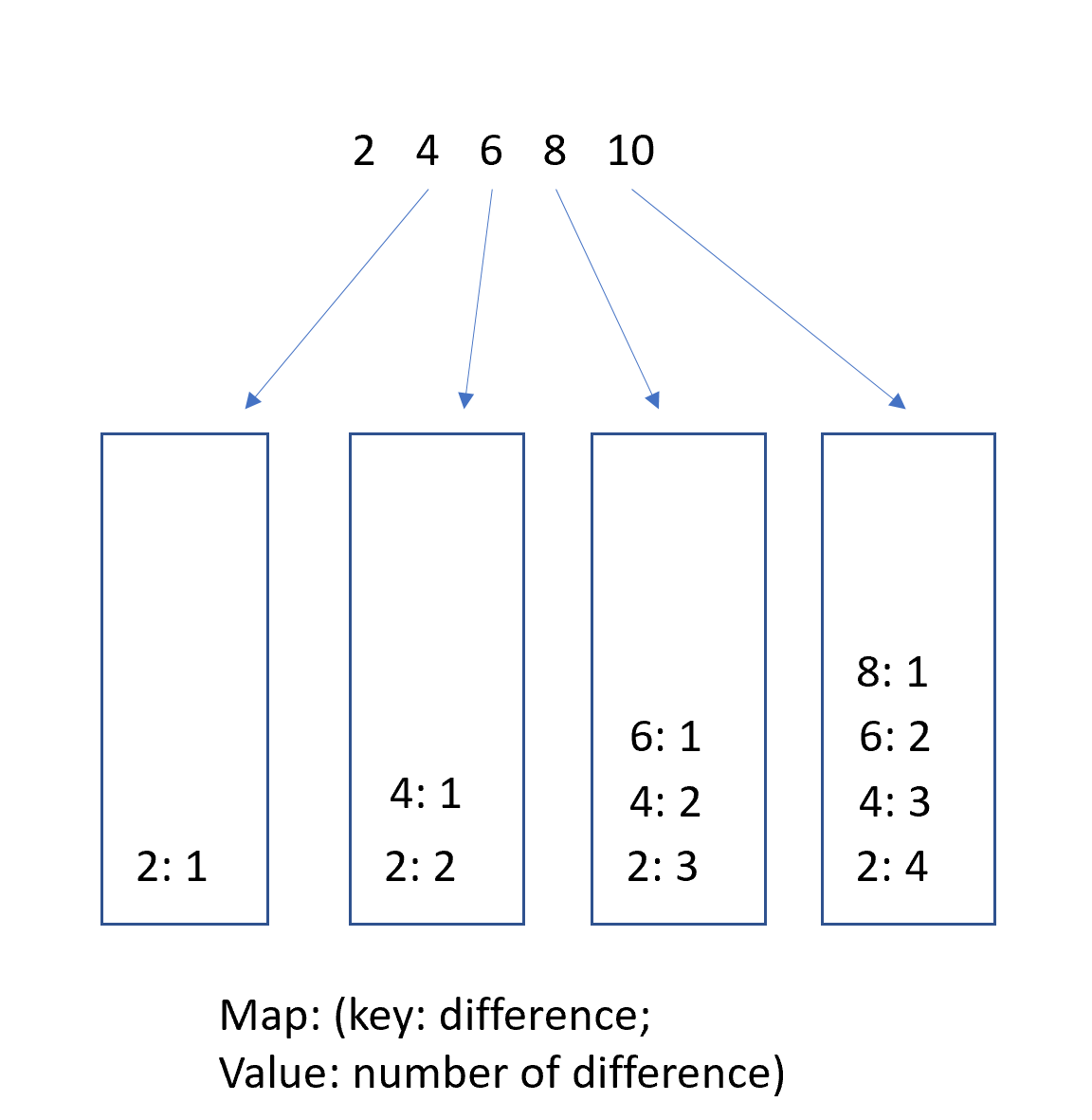
How many subsequence we can form with the new element?

If we know at element \(8\), we have \(k\) difference, then \(10\) will form \(k\) new subsequence, because we can form: 2, 4, 6, 8, 10 4, 6, 8, 10 6, 8, 10

That is: we can join \(10\) to form a new sequence, and drop \(k-1\) previous element to form another \(k-1\) subsequence. Why \(k-1\)? Because we need at least \(2\) difference to form an arithmetic subsequence.

How should we update the HashMap?

The Map records the total number of difference until current element. It should be added by 1. I.e., \(diff_i += diff_j + 1\) for every precede element j, with the same diff value;

     public int numberOfArithmeticSlices(int[] nums) {
        int n = nums.length;
        
        Map<Long, Integer> [] count = new HashMap[n];
        for (int i = 0; i < n; i++) 
            count[i] = new HashMap<>();
        int total = 0;
        for (int i = 1; i < n; i++)
            for (int j = 0; j < i; j++) {
                long diff = (long)nums[i]-(long)nums[j];
                
                int prevCount = count[j].getOrDefault(diff,0);
                // preserve current count, because different j could generate the same value difference.
                int curCount = count[i].getOrDefault(diff, 0);
                count[i].put(diff, prevCount + curCount + 1);
                total += prevCount;
            }

        return total;
    }