Algorithm & Data Structure - Palindromic substring
Palindromic substring is a hot topic in string handling problem. A series of problems are related to palindromic string or substring.
Verify palindromic string
- LeetCode - 125, 680
These two problems are relatively simple, both loop and recursive methods could be used, but recursive could result in much slow comparing to loop method.
Longest palindromic substring
- LeetCode - 5, 214
An inuitive approach is to check the longest palindromic substring of each character. This takes O(N^2) time. There are some other approaches that could take O(nlogn) or O(n). A classical approach is Manacher’s Algorithm. The basic inuation behind Manacher’s algorithm is to use the information we have gotten before. Take below string as an example,
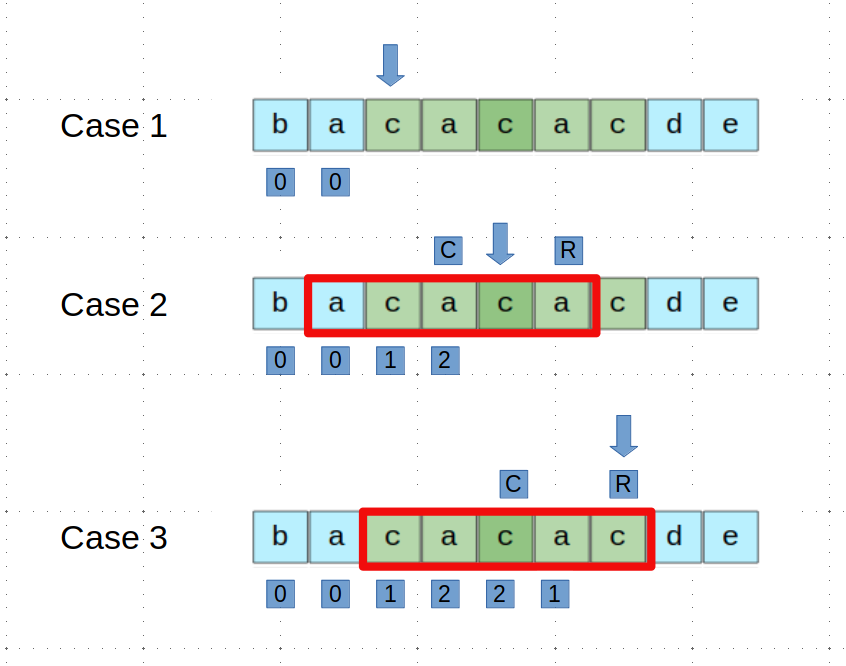
Case 1
The current char is not in the range of any previous palindromic substring. We have to expand from the current char to find the palindromic substring.
Case 2
The current char is in the range of the previous palindromic substring with center index of C, it could expand to maximum index of R, which is C+2 in this case. Because of the symmetric property, the palindromic substring of current char is at least similar to its mirror character. In this case, the mirror char has an expand length of L, and i+L < R, so we can expand from i+L.
Case 3
This case is similar to Case 2, but the mirror char has an expand length of i + L > R. We can’t expand from i+L directly but only from R.
To simplify the index and odd or even length of string, we could insert character to every char in the string.
public String longestPalindrome(String s) {
// insert | to the string
int n = s.length();
char[] sc = new char[2*n+1];
for (int i = 0; i+1 < sc.length; i+=2) {
sc[i] = '|';
sc[i+1] = s.charAt((i+1)/2);
}
sc[sc.length-1] = '|';
// expand length of every char
int[] length = new int[sc.length];
int rightMost = 0, center = 0;
int maxLength = 0, maxPos = 0;
for (int i = 1; i < sc.length; i++) {
int left = i, right = i;
// if current char is in the range of previous expand, use the mirror expand length
if (i <= rightMost) {
right = Math.min(i + length[2*center - i], rightMost);
left = 2*i - right;
}
// expand
while (left >= 0 && right < sc.length) {
if (sc[left] == sc[right]){
left--;
right++;
} else {
break;
}
}
// update center and max expand
if (right-1 > rightMost) {
rightMost = right-1;
center = i;
}
length[i] = right - 1 - i;
if (length[i] > maxLength) {
maxLength = length[i];
maxPos = i;
}
}
StringBuilder res = new StringBuilder();
for (int i = maxPos - maxLength; i <= maxPos+maxLength; i++){
if (sc[i] != '|')
res.append(sc[i]);
}
return res.toString();
}
LeetCode 214 could also use Manacher’s algorithm, but note that we need to find the longest palindomic string including the first char. And the search could stop when reaching the center of the string.
public String shortestPalindrome(String s) {
int n = s.length();
char[] sc = new char[2*n+1];
for (int i = 0; i+1 < sc.length; i+=2){
sc[i] = '|';
sc[i+1] = s.charAt((i+1)/2);
}
sc[sc.length-1] = '|';
int [] length = new int[sc.length];
int rightMost = 0, center = 0;
int maxLength = 0, maxPos = 0;
for (int i = 1; i < sc.length; i++){
int left = i, right = i;
if (i <= rightMost) {
right = Math.min(rightMost, i+length[2*center-i]);
left = 2*i - right;
}
while (left >= 0 && right < sc.length) {
if (sc[left] == sc[right]) {
left--;
right++;
} else {
break;
}
}
length[i] = right - i - 1;
if (right - 1 > rightMost) {
center = i;
rightMost = right-1;
}
if (left <= 0 && length[i] > maxLength) {
maxPos = i;
maxLength = length[i];
}
}
StringBuilder res = new StringBuilder();
for (int i = sc.length-1; i > maxPos+maxLength; i--) {
if (sc[i] != '|') {
res.append(sc[i]);
}
}
for (int i = 0; i < sc.length; i++) {
if (sc[i] != '|') {
res.append(sc[i]);
}
}
return res.toString();
}
