Algorithm & Data Structure - Range Sum and Segment Tree
Segment Tree is used for immutable range sum query and update.
- LeetCode - 303 304 307 308
For immutable range sume query like Leetcode 303 and 304, we could precalculate the presum at every node (takes O(n)), and return query with the sum of the range by simply substract the index of the presum, e.g., range (i, j) = presum[j] - presum[i-1]. That takes O(1) for each query. Similary approach for 2D matrix immutable range sum.
For mutable range sum query like Leetcode 307 and 308. If we continue use the presum approach, we still could get O(1) for every query. But we need to take O(n) to recalculate the presum when update element.
#### Can we do better?
There are two algorithms that could reduce the update time, segment tree and Binary Index Tree. Both of them could get O(logN) on update and query. We will use segment tree as it is easier to understand.
The basic idea of segment tree is to divide the array or matrix into different segment, each segment maintains its own range sum. For array segment, each node has two children, and each of the child maintain a sub range sum (normally divided in the middle). The root of the tree has the sum of the whole array, and the leaves has element value.
When we query range sum, we need to match the query range and segment range, if they match, simply return the sum. If not, we go to its children to find the sum.
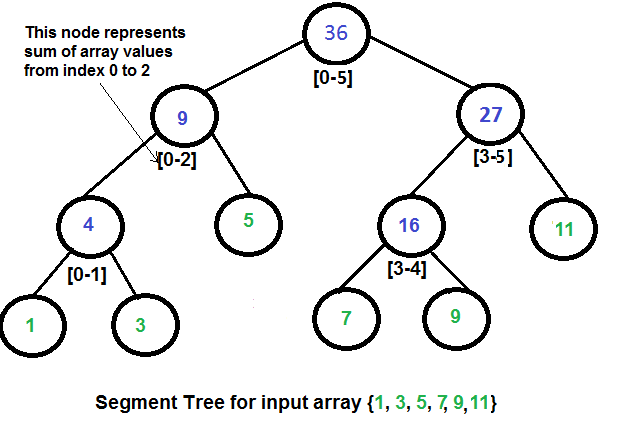
Take the above tree as example:
- If query [0, 2], then we go the second left node and we get matched.
- If query [0, 4], then we have to divide it to be [0, 2] and [3, 4], and go to left and right children respectively. Overall, it takes O(logN) to get a match which is the height of the tree.
For Update, we have to go down to the leave and update the element. Notice that whenever an element is updated, its parent node need to be updated too, becase the parent node is the sum of its children node.
private static class SegmentNode {
int minId, maxId, sum;
SegmentNode left, right;
SegmentNode(int min, int max, int val){
minId = min;
maxId = max;
sum = val;
}
SegmentNode(){}
}
private SegmentNode buildTree(int i, int j, int[] arr){
if (i == j) {
return new SegmentNode(i,i,arr[i]);
}
int mid = i + (j-i)/2;
SegmentNode root = new SegmentNode();
root.minId = i;
root.maxId = j;
root.left = buildTree(i, mid, arr);
root.right = buildTree(mid+1, j, arr);
root.sum = root.left.sum+root.right.sum;
return root;
}
private void updateNode(SegmentNode p, int k, int val){
if (p.minId == k && p.maxId == k) {
p.sum = val;
return;
}
int mid = p.minId + (p.maxId-p.minId)/2;
if (k > mid) {
updateNode(p.right, k, val);
} else {
updateNode(p.left, k, val);
}
// update parent node sum
p.sum = p.left.sum + p.right.sum;
}
private int rangeSum(SegmentNode p, int i, int j){
if (p == null || i > j || i > p.maxId || j < p.minId) return 0;
if (i== p.minId && j == p.maxId) {
return p.sum;
}
int mid = p.minId + (p.maxId-p.minId)/2;
int sum = 0;
sum += rangeSum(p.left, i, Math.min(mid, j));
sum += rangeSum(p.right, Math.max(mid+1, i), j);
return sum;
}
2D Range Sum
2D mutable range sum is a bit more complext, but the basic idea is the same. This time, we need to divede the matrix into 4 segments. Each of them maintains the sum of its own segment and four children - leftUp, leftBot, rightUp, rightBot.
private static class SegmentNode {
int rowMin, rowMax, colMin, colMax;
int val;
SegmentNode leftUp, leftBot, rightUp, rightBot;
SegmentNode(int rMin, int rMax, int cMin, int cMax, int v) {
rowMin = rMin;
rowMax = rMax;
colMin = cMin;
colMax = cMax;
val = v;
}
}
private SegmentNode buildTree(int[][] m, int rMin, int rMax, int cMin, int cMax) {
if (rMin > rMax || cMin > cMax) return null;
if (rMin == rMax && cMin == cMax) {
return new SegmentNode(rMin, rMax, cMin, cMax, m[rMin][cMin]);
}
int rMid = rMin + (rMax-rMin)/2;
int cMid = cMin + (cMax-cMin)/2;
SegmentNode p = new SegmentNode(rMin, rMax, cMin, cMax, 0);
p.leftUp = buildTree(m, rMin, rMid, cMin, cMid);
p.rightUp = buildTree(m, rMin, rMid, cMid + 1, cMax);
p.leftBot = buildTree(m, rMid+1, rMax, cMin, cMid);
p.rightBot = buildTree(m, rMid+1, rMax, cMid +1, cMax);
updateSum(p);
return p;
}
private void updateSum(SegmentNode p) {
// the segment might have only two segments, so need to check whether it is null
if (p.leftUp != null) {
p.val += p.leftUp.val;
}
if (p.leftBot != null) {
p.val += p.leftBot.val;
}
if (p.rightUp != null) {
p.val += p.rightUp.val;
}
if (p.rightBot != null) {
p.val += p.rightBot.val;
}
}
private void update(SegmentNode p, int r, int c, int v) {
if (p == null || r < p.rowMin || r > p.rowMax || c < p.colMin || c > p.colMax) {
return;
}
if (r == p.rowMin && r == p.rowMax && c == p.colMin && c == p.colMax) {
p.val = v;
return;
}
int rMid = p.rowMin + (p.rowMax-p.rowMin)/2;
int cMid = p.colMin + (p.colMax-p.colMin)/2;
update(p.leftUp, r, c, v);
update(p.rightUp, r, c, v);
update(p.leftBot, r, c, v);
update(p.rightBot, r, c, v);
p.val = 0;
updateSum(p);
}
private int getSum(SegmentNode p, int rMin, int rMax, int cMin, int cMax) {
if (p == null || rMin > rMax || cMin > cMax) return 0;
if (rMin == p.rowMin && rMax == p.rowMax && cMin == p.colMin && cMax == p.colMax) {
return p.val;
}
int rMid = p.rowMin + (p.rowMax-p.rowMin)/2;
int cMid = p.colMin + (p.colMax-p.colMin)/2;
int sum = 0;
sum += getSum(p.leftUp, rMin, Math.min(rMax, rMid), cMin, Math.min(cMax, cMid));
sum += getSum(p.rightUp, rMin, Math.min(rMax, rMid), Math.max(cMin, cMid +1), cMax);
sum += getSum(p.leftBot, Math.max(rMid+1, rMin), rMax, cMin, Math.min(cMax, cMid));
sum += getSum(p.rightBot, Math.max(rMid+1, rMin), rMax, Math.max(cMin, cMid +1), cMax);
return sum;
}
