This is a series of six problems in stock buy and sell. All of them could be solved by dynamic programming.

• LeetCode - 121

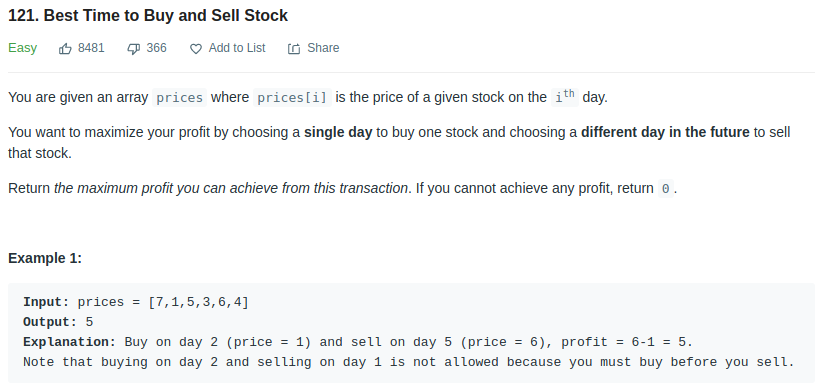
This problem applies the principle: buy low, sell high. We basiclly need to find the maximum difference between those prices, i.e: price[highId] - price[lowId], but with one constraints, highId > lowId, i.e., we can only sell after buy. Naively, we can use two for loop to find the maximum difference, i.e.,

    for (int i = 1; i < n; i++) {
        for (int j = 0; j < i; j++){
            max_profit = Math.max(max_profit, prices[i]-prices[j]);
        }
    }

These loops take O(n^2). Consider how can we optimize it, when we move i forward, we restart j from 0 for every time, which is not nessacerry. We could safely reuse the information from the previous loop, i.e, i-1, because we only add one more element i to it. Because we are calculating the maximum difference, we can thus preserve the minimum price so far, and for every i, we update both the minimum price and maximum difference.

    int minPrice = prices[0];
    int max_profit = 0;
    for (int i = 1; i < n; i++){
        max_profit = Math.max(max_profit, prices[i] - minPrice);
        minPrice = Math.min(prices[i], minPrice);
    }

• LeetCode - 122

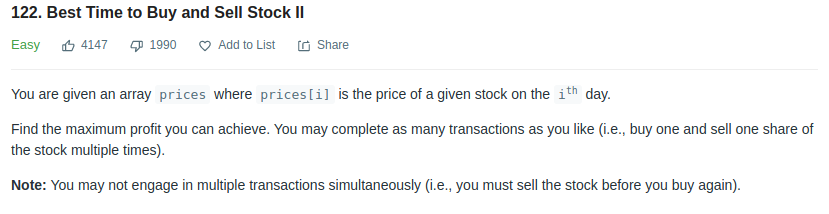
Since we can transact as many times as possible, we can take buy and sell when there is profit. That means whenever we see a positive increment in any time, we simply take the profit.

    int max_profit = 0;
    for (int i = 0; i < prices.length - 1; i++) {
        if (prices[i+1] - prices[i] > 0) {
            max_profit += prices[i+1] - prices[i];
        }
    }

• LeetCode - 714

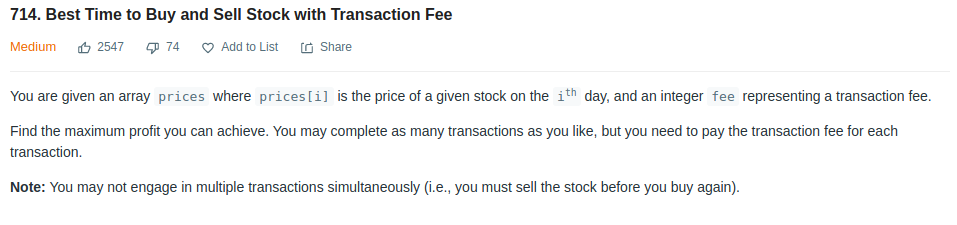
With transaction fee, we can’t take profit simply as LeetCode - 122. We have to hold stock long enough to be profit. We have two states now, we hold the stock or we sell it. We can use dynamic array to record the profit of these two states every day.

1. If we hold the stock, we either bought it yesterday, or we buy it today, the profit is the maximum of them.
2. If we sell the stock, we eigher sold it yesterday, or we sell it today, the profit the maximum of them.

    int n = prices.length;

    int [][] dp = new int[n][2];
    dp[0][0] = -prices[0];

    for (int i = 1; i < n; i++) {
        dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]-prices[i]);
        dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i] - fee);
    }

We could also use the same approach for the previous two problems.

• LeetCode - 309

With cooldown, this is more like a dynamic programming problem. We have three states now, each of the states depends on the previous day’s state. We have buy, cooldown and sell. Consider how these three states change profit today. We define a dynamic array as dp[n][3], where 0 represents buy, 1 represent cooldown, and 2 represent sell.

1. If we buy today, we either already bought yesterday or yesterday is cooldown day. So the profit with this state is the maximum of them, i.e., dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i]);
2. If we cooldown today, either yesterday is cooldown too or yesterday is a sell day. So the profit with this state is the mainimum of them, i.e., dp[i][1] = max(dp[i-1][1], dp[i-1][2]);
3. If we sell today, either yesterday is already a sell day or yesterday is a buy day, so the profit with this state is the maximum of them, i.e., dp[i][2] = max(dp[i-1][2], dp[i-1][0]+prices[i]);

With these transition, we can write the code as below:

    int n = prices.length;
    int [][] dp =  new int[prices.length][3];
    dp[0][0] = - prices[0];

    for (int i = 1; i < prices.length; i++) {
        dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] - prices[i]);
        dp[i][1] = Math.max(dp[i-1][2], dp[i-1][1]);
        dp[i][2] = Math.max(dp[i-1][2], dp[i-1][0]+prices[i]);
    }

    return Math.max(dp[n-1][1], dp[n-1][2]);

• LeeCode - 123 188

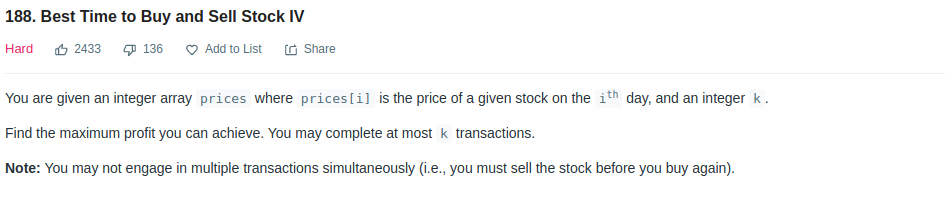
These two problems are the same, we can use the same approach. Using dynamic programming, we preserve profit at ith day and kth transaction as dp[i][k]. The question is how do we make state transition. For the 0th transcation, no profit could be generated. For the kth transcation, we already know the profit at k-1 th transaction. We could use these information to obtain the profit at kth transaction. Since we already know the k-1th profit, at ith day, we need to use the profit of k-1th until i-1 day. We want to make another transaction at ith day, so we need to buy at some day between 0 to i-1 day, and sell at ith day. We could loop through 0 to i-1 and find the maximum profit. Take the below prices as example.

    3 2 5 6 0 3
  0 0 0 0 0 0 0
  1 0 0 3 4 4 4
  2 0 0 3 4 4 ?

A typical dynamic program would be:

    int n = prices.length;
    int [][] dp =  new int[n][k+1];

    
    for (int j = 0; j < k+1; j++) 
        for (int i = 1; i <  n; i++) {
            
            for (int p = 0; p < i; p++){
                dp[i][j] = Math.max(dp[i][j], prices[i] - prices[p] + dp[p][j-1]);
            }
        }

The above code takes about O(kn^2); As in problem 1 above, we could optimize the max function in the inner loop. *- prices[p] + dp[p][j-1] this part could be reuseable. We maintain the maximum value of it and update it for every i.

     int n = prices.length;
    int [][] dp =  new int[n][k+1];
    
    for (int j = 0; j < k+1; j++) {
        int maxProfit = - prices[0] + dp[0][j-1];
        for (int i = 1; i <  n; i++) {
            dp[i][j] = Math.max(dp[i-1][j], prices[i] + maxProfit);
            maxProfit = Math.max(maxProfit, - prices[i] + dp[i][j-1]);  
        }
    }

This algorithm now is O(k*n).