Algorithm & Data Structure - Monotonic Stack
Monotonic stack is a stack that maintain the element in the stack with increasing or decreasing property, i.e., when poping element from the stack, the elements are in sorted order. This property itself seems useless, but it can be used to solve some of the problems in LeetCode.
- LeetCode - 496, 503, 1019, 84, 85
Next Greater Element
Q: Find the next greater element of all the elements in a given array, if none, return -1.
Example: Given nums = [1, 3, 4, 2], the next greater elements are res = [3, 4, -1, -1].
Intuitatively, we could loop all element after the current element and find the first element that larger than the current one and return. For all elements, it takes O(n^2) time complexity.
Can we do better?
In the previous approach, we loop from the begining, and for ith element, we search from i + 1 element to the end of array. So the elements from i+2 to end are repeatly searched, which is waste of time. Can we store these elements for later use, and how?
Approach 1
Instead of thinking who is the next greater one of current element, thinking whose next greater is me when reaching the current element. So we can store the elements until the ith one in the stack, once we see the element in the stack is less than the current element, that means, it is the next greater element of the one in the stack. Pop out all the element from the stack that is less than the current one, and set their next greater as the current one, and push the ith element. The stack is naturally maintained as a decreasing stack. When finishing all the elements from the array, pop all elements from the stack and set their next greater as -1. If we can preset the result as -1, then we can leave it. Picture below shows the stack change of this process.
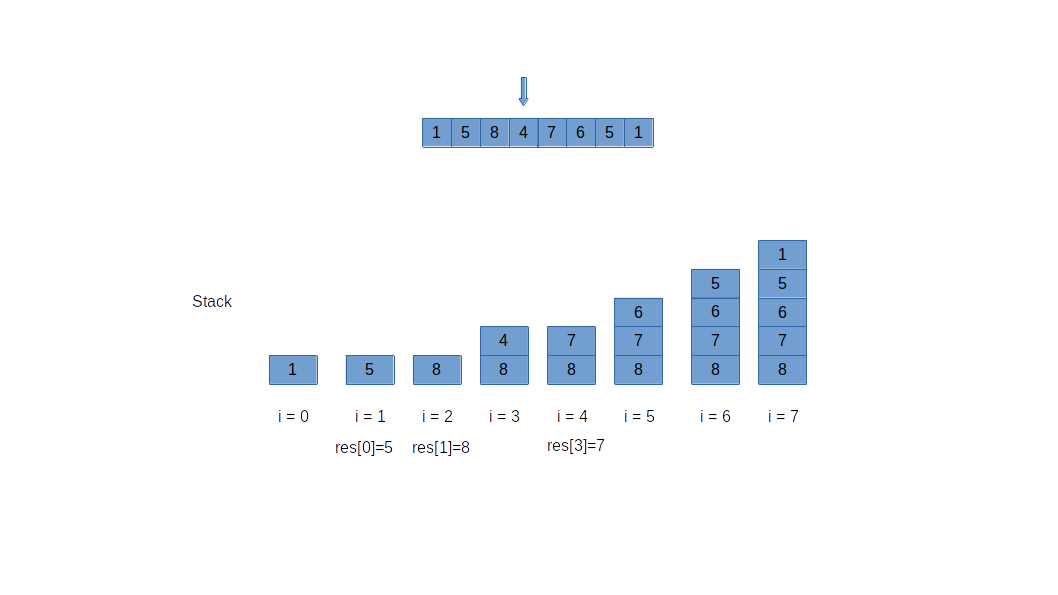
Approach 2
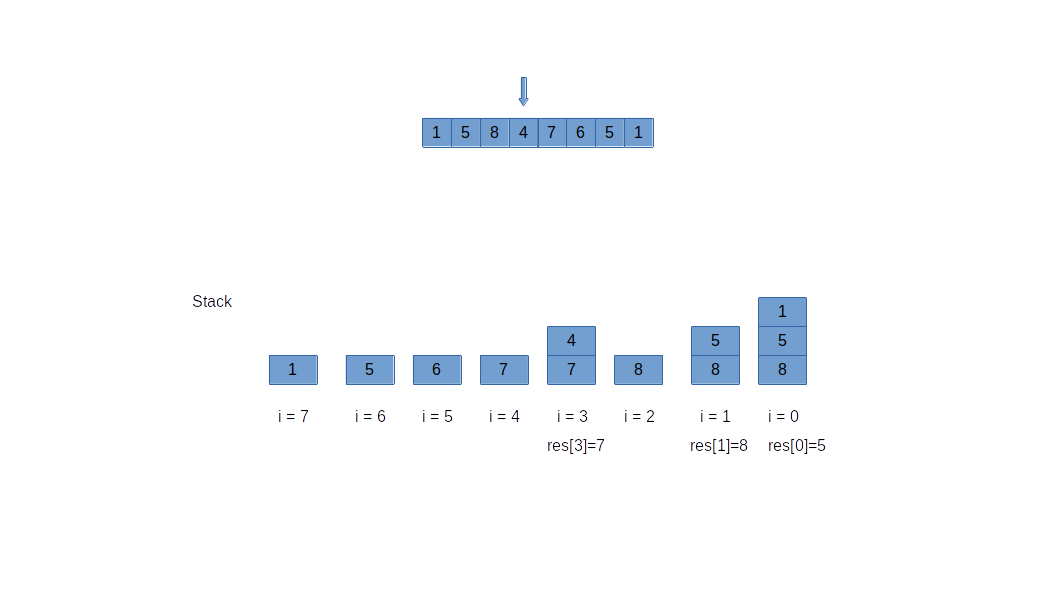
Another way is to loop from the end of the array. For the ith element, pop out from stack until one is more than the ith element, set the next greater of ith. If not found one, then the next greater is -1. Push the ith element into stack. This way, the stack is maintained as decreasing order.
Both the above approaches take O(n), because every element is pushed and poped maximum only once. Picture below shows this process.
Core Code:
// core code for the first apprach - monotonic decreasing stack.
public int[] nextGreaterElement(int[] nums) {
int [] res = new int[nums.length];
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < nums.length; i++) {
res[i] = -1; //first set it to -1
while(!stack.isEmpty() && nums[stack.peek()] < nums[i]){
res[stack.pop()] = nums[i];
}
stack.push(i); // need to remember the index
}
}
// core code for the second apprach - monotonic increasing stack.
public int[] nextGreaterElement(int[] nums) {
int [] res = new int[nums.length];
Stack<Integer> stack = new Stack<>();
for (int i = nums.length - 1; i >= 0; i--) {
res[i] = -1; //first set it to -1
while(!stack.isEmpty() && stack.peek() <= nums[i]){
stack.pop();
}
if (!stack.isEmpty()) {
res[i] = stack.peek();
}
stack.push(nums[i]); // could push the number directly, also could push the index
}
}
LeetCode 496 503 1019
These are minor variatio of the approach above, for 496, an map could be added to record the next element and later extracted to the result. Ror 503, traditional way to treat rotational array, add the same array to the end of the array, or initialize the stack by push all element from the array. For 1019, only the first approach could be used, because linked list cannot be traversed from the end.
LeetCode 84
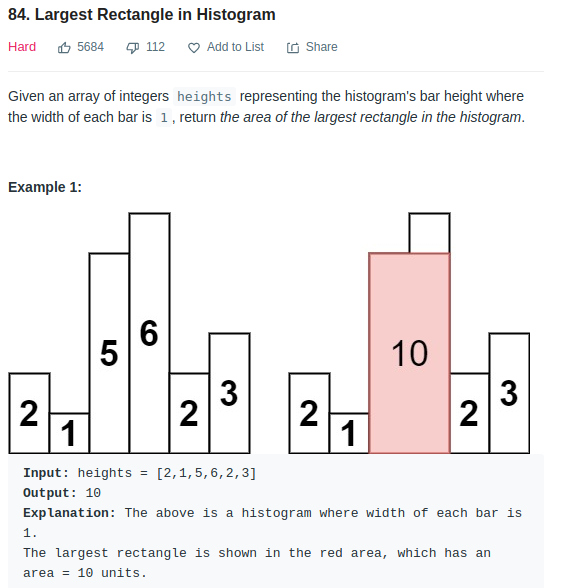
The stack approach could be used to improve the time complexity of this problem. First, let’s look at the brutal force way.
Brutal Force
For each of the element, we can expand from left and right, and find the first element less than the current one. The area is then heights[i] x (right - left - 1). This requires O(n^2).
Stack approach
From the brutal force solution, we observed that we are actually looking for the next smaller element from both sides of the current element. We were talking about looking for next greater element before.
What can we do to look for next smaller element?
It is similar to Approach 1, loop from the begining, we maintain a stack. For current ith element, pop out the element more than the ith element, their next smaller element is ith element. Push ith element into stack. This way, the stack is a monotonic inceasing stack. But it seems we only find the next smaller element on the right side. How about the left side?
We can use the stack to find the left smaller element. The stack maintains increasing order. That means the next poped element is less than the previous poped element. All the elements in between must be more than the peek element, and so there width could be used to calculate the area.
Coner case
When we loop through all the elements, there will be one last element that is the minimum value and it’s width should cover the length of the array. But it will not have the oppurtunity to be poped out. For example, in the above example, number 1 is not going to pop out, because no element is less than it. Element 2 is also not going to pop out, because no element is less than 2 after it. How should we handle these corner cases?
To pop out these two elements, we need another two elements that are less than than, and we need to cover the width. To cover the whole length of array, we can add element 0 to both ends of the array, and treat them as a element, i.e., expand the array and add these two elements.
public int largestRectangleArea(int[] heights) {
int[] newHeights = new int[heights.length + 2];
// add two elements to the two ends and form a new array.
for (int i = 0; i < heights.length; i++) {
newHeights[i+1] = heights[i];
}
Stack<Integer> stack = new Stack<>();
int maxArea = 0;
for (int i = 0; i < newHeights.length; i++) {
while (!stack.isEmpty() && newHeights[stack.peek()] > newHeights[i]) {
int cur = stack.pop();
int width = i - stack.peek() - 1;
maxArea = Math.max(maxArea, newHeights[cur] * width);
}
stack.push(i);
}
return maxArea;
}
LeetCode 85
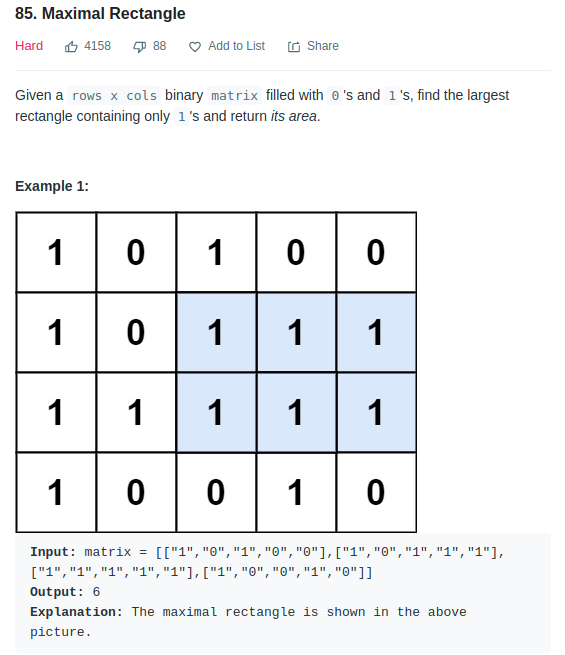
Initially, I though DP might be a solution, the state transfer is a little complex.
For each row, we only need to calculate the maximum area until that row. Treat the column as the height for each row, it is then similar to 85. An addition task is to calculate the height of each column and each row. The column height is the number of 1s at that column starting from the row. Any 0 in between can’t be count.
Code as below:
public int maximalRectangle(char[][] matrix) {
if (matrix.length == 0) return 0;
int m = matrix.length, n = matrix[0].length;
int[][] colSum = new int[m][n+2];
// calculate column sum for each of the column and row
for (int j = 0; j < n; j++)
colSum[0][j+1] = matrix[0][j]-'0';
for (int i = 1; i < m; i++) {
for (int j = 0; j < n; j++)
{
if (matrix[i][j] == '0') {
colSum[i][j+1] = 0;
} else {
colSum[i][j+1] = colSum[i-1][j+1] + 1;
}
}
}
Stack<Integer> stack = new Stack<>(); // monotonic increasing stack
int maxArea = 0;
for (int i = 0; i < m; i++) {
stack.clear();
for (int j = 0; j < n+2; j++) {
while(!stack.isEmpty() && colSum[i][stack.peek()] > colSum[i][j]) {
int cur = stack.pop();
int width = j - stack.peek() - 1;
maxArea = Math.max(maxArea, colSum[i][cur]*width);
}
stack.push(j);
}
}
return maxArea;
}
Leetcode - 1944
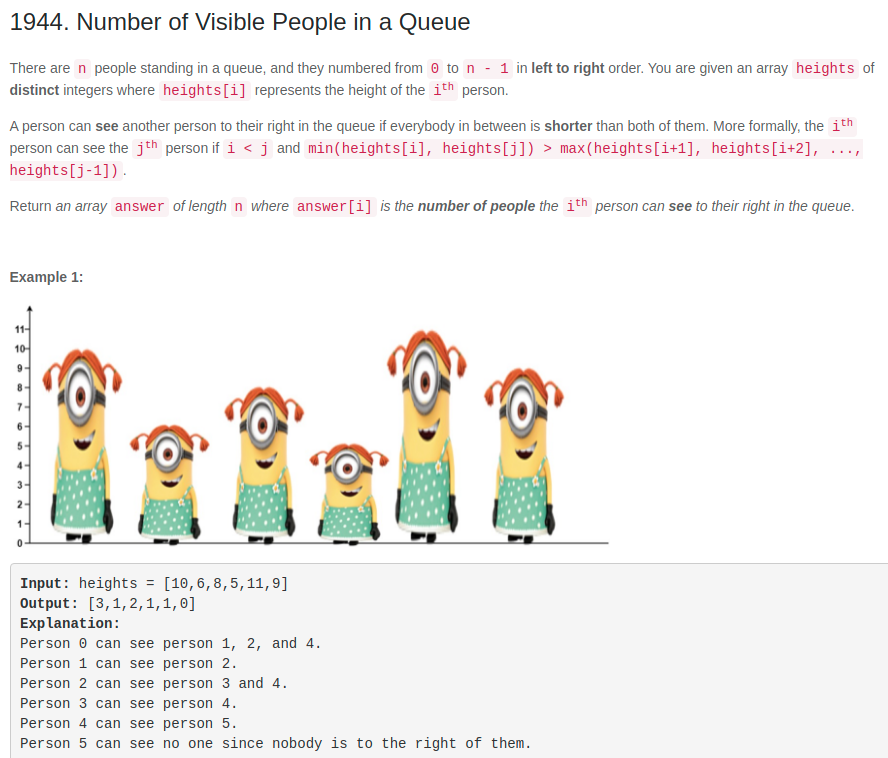
Brutal force would be to scan every j > i and test if i could see j. If a height[j] is more than height[i], then we can stop scan. We also need to keep maximum height after hiehgt[i], and if height[j] is less than maximum height sofar, then i can’t see j. This takes O(n^2).
for (int i = 0; i < n; i++) {
int maxHeight = 0;
for (int j = i+1; j < n ; j++) {
if (heights[j] > maxHeight) {
res[i]++;
maxHeight = heights[j];
}
if (heights[j] > heights[i]) {
break;
}
}
}
We are actually looking the next greater height in this problem. Obviously, any previous height that is less than current height could see current one. We could use monotonic stack to maintain a descreasing stack, and:
- If the top height is less than current height, then the top height could see the current height;
- When we push the current height into stack, the top element in the stack could also see the current height.
public int[] canSeePersonsCount(int[] heights) {
int n = heights.length;
Stack<Integer> stack = new Stack<>();
int[] res = new int[n];
for (int i = 0; i < n; i++) {
while(!stack.isEmpty() && heights[stack.peek()] < heights[i]) {
int prev = stack.pop();
res[prev] += 1;
}
if (!stack.isEmpty() ) {
res[stack.peek()]++;
}
stack.push(i);
}
return res;
}
### Leetcode - 316
The basic idea is to try to build a increasing string. Therefore, if we see a character \(c_i\), we try to put it into the result string. When later we find a smaller character and we still have \(c_i\) left, we could remove \(c_i\). This idea is similar to monotonic stack that we pop out all previous \(c_i\) with some conditions. This leads us to use monotonic stack:
public String removeDuplicateLetters(String s) {
int[] count = new int[26];
boolean[] visited = new boolean[26];
// firstly, count the number of occurance of each letter
for (int i = 0; i < s.length(); i++) {
count[s.charAt(i)-'a']++;
}
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
// reduce the number of occurance of current letter
count[c-'a']--;
//if it is already in the stack, skip it.
if (visited[c-'a']) continue;
while(!stack.isEmpty()) {
// pop out all previous bigger character that still has count later
// set them to be unvisited.
if (stack.peek() > c && count[stack.peek()-'a'] > 0) {
visited[stack.peek()-'a'] = false;
stack.pop();
} else {
break;
}
}
//temporary push the current char to stack
stack.push(c);
visited[c-'a'] = true;
}
StringBuilder sb = new StringBuilder();
while(!stack.isEmpty()) {
sb.insert(0,stack.pop());
}
return sb.toString();
}